1 Chalkboard
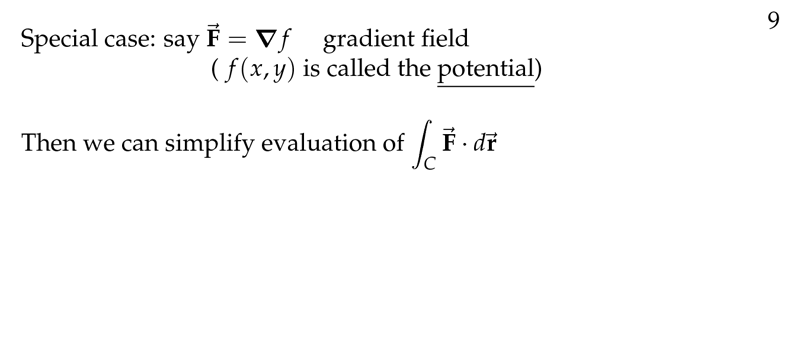
Figure 1: Special case where vector field is gradient field

Figure 2: Fundamental Theorem of Calculus for Line Integrals

Figure 3: Proof of FTC for Line Integrals
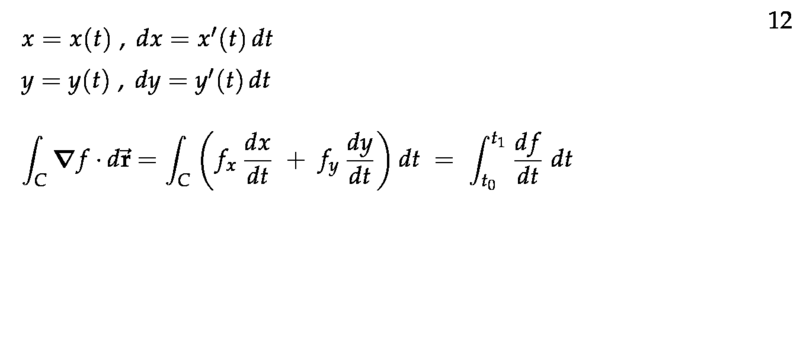
Figure 4: Proof of FTC for Line Integrals - 2
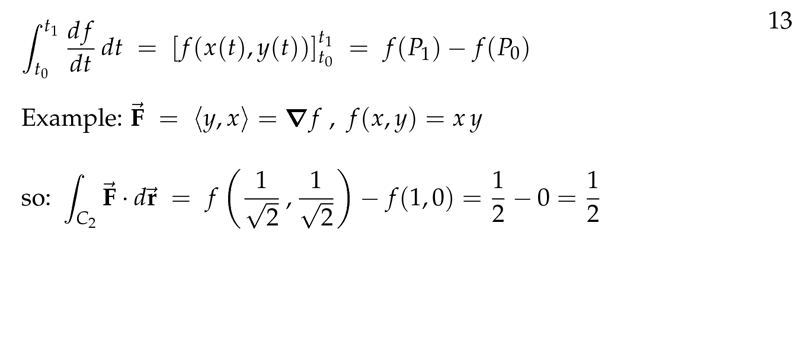
Figure 5: Example of FTC for Line Integrals

Figure 6: Warning: Only for gradient fields
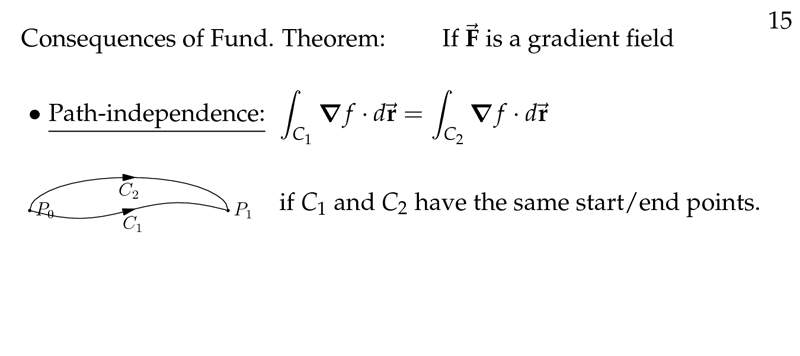
Figure 7: Path independence
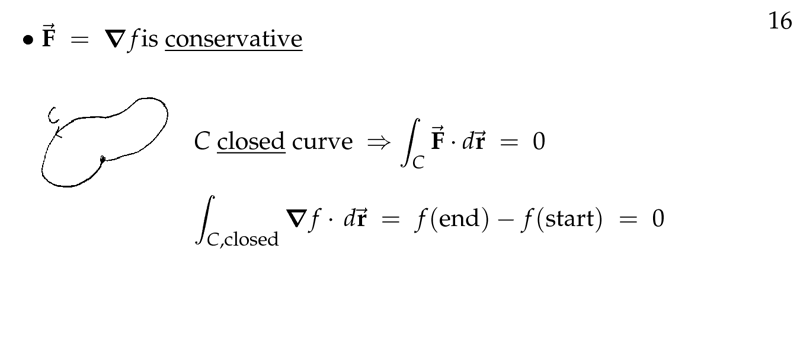
Figure 8: Gradient field is conservative
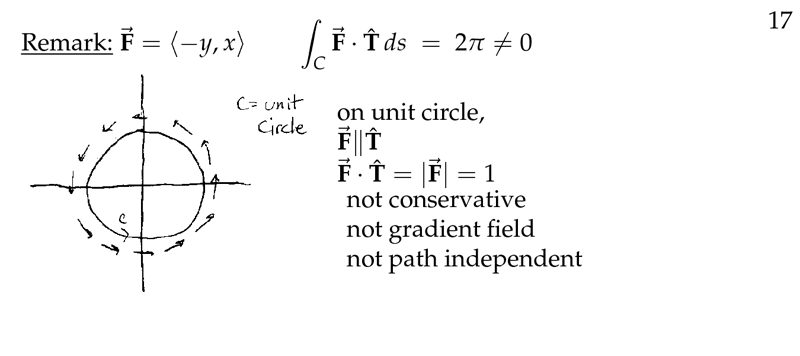
Figure 9: Non-conservative vector field
2 Describe the Fundamental Theorem of Calculus for Line integrals
2.1 Front
Describe the Fundamental Theorem of Calculus for Line integrals
\(\vb{F}\) and \(C\) any curve
2.2 Back
\(\vb{F} = \grad{f}\) is a gradient field, and \(C\) is any curve with endpoint \(P_0 = (x_0,y_0)\) and \(P_1 = (x_1, y_1)\)
\({\displaystyle \int_C \vb{F} \dd{\vb{r}} = \eval{f(x,y)}_{P_0}^{P_1} = f(x_1, y_1) - f(x_0, y_0)}\)
That is, for gradient field the line integral is independent of the path taken, i.e., it depends only on the endpoints of \(C\)
3 How can we proof FTC for Line integrals?
3.1 Front
How can we proof FTC for Line integrals?
\(\vb{F}\) and \(C\) any curve
3.2 Back
\(\vb{F} = \grad{f}\) is a gradient field and \(f(x,y)\) is a potential function. The curve is defined by a parametric curve where \(x = x(t)\) and \(y = y(t)\). Where \(t_0\) is the start endpoint and \(t_1\) is the finish endpoint of the curve \(C\)
\({\displaystyle \int_C \grad{f} \dd{\vb{r}} = \int_C f_x \dd{x} + f_y \dd{y} = \int_{t_0}^{t_1} \biggl[ f_x(x(t), y(t))\dv{x}{t} + f_y(x(t), y(t)) \dv{y}{t} \biggr] \dd{t}}\) (From the chain rule)
\({\displaystyle = \int_{t_0}^{t_1} \dv{f(x(t), y(t))}{t} \dd{t} = \eval{f(x(t), y(t))}_{t_0}^{t_1} = f(P_1) - f(P_0)}\)
4 What means the FTC for Line Integral?
4.1 Front
What means the FTC for Line Integral?
\(\vb{F}\) and \(C\) any curve
Describe the consequences
4.2 Back
\(\vb{F} = \grad{f}\) (gradient field)
For gradient fields \(\vb{F}\) the work integral \({\displaystyle \int_C \vb{F} \dd{\vb{r}}}\) depends only on the endpoints of the path. In this case a line integral is path independent
Special case, for closed curve \(C\)
\({\displaystyle \oint_C \grad{f} \dd{\vb{r}} = 0}\) (no work)
Following physics, where a conservative force does no work around a closed loop, we say \(\vb{F} = \grad{f}\) is a conservative field.
5 All vector fields are gradient fields?
5.1 Front
All vector fields are gradient fields?
5.2 Back
No
6 Can we apply FTC for Line integral to any vector field?
6.1 Front
Can we apply FTC for Line integral to any vector field?
6.2 Back
No, we only can apply for gradient fields, so \(\vb{F} = \grad{f}\)
7 What can we say about this equation?
7.1 Front
What can we say about this equation?
\({\displaystyle \oint_C \vb{F} \dd{r}}\), where \(\vb{F} = \grad{f}\)
7.2 Back
We can say that \(\vb{F}\) is a conservative force that does no work around a closed loop, so \({\displaystyle \oint_C \grad{f} \dd{\vb{r}} = 0}\)
8 Write the FTC for Line integrals using differentials
8.1 Front
Write the FTC for Line integrals using differentials
\(\vb{F}\) and \(C\) any curve
8.2 Back
\(\vb{F} = \grad{f} = \ev{f_x,f_y} \implies \grad{f} \dd{r} = \ev{f_x,f_y} \cdot \ev{\dd{x},\dd{y}} = f_x \dd{x} + f_y \dd{y}\)
Using differentials \(\dd{f} = f_x \dd{x} + f_y \dd{y}\)
\({\displaystyle \int_C M \dd{x} + N \dd{y} = \int_C df}\), where \(M = f_x\) and \(N = f_y\)
\(\int_C \dd{f} = f(P_1) - f(P_0)\), where \(P_0\) and \(P_1\) are the endpoints of the curve \(C\)