1 Chalkboard
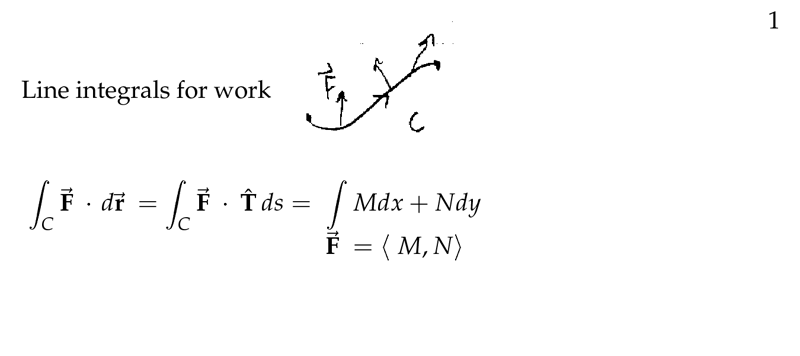
Figure 1: Line integrals for work
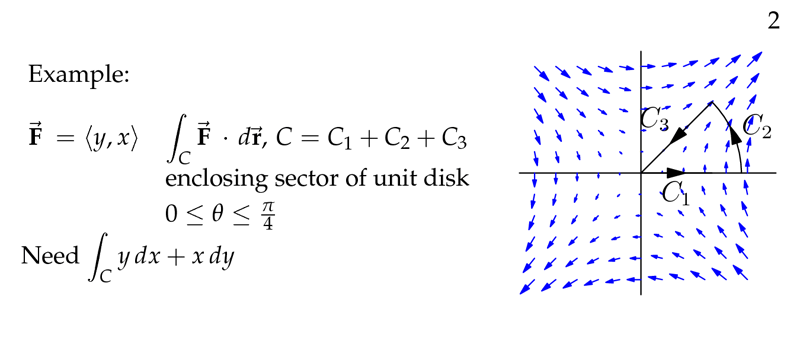
Figure 2: Example of line integrals for work
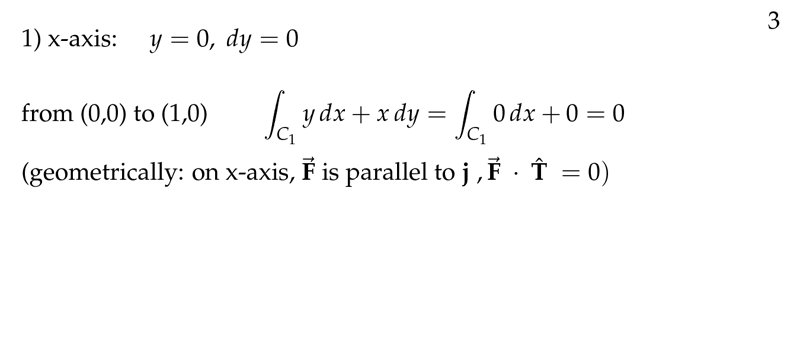
Figure 3: First trajectory
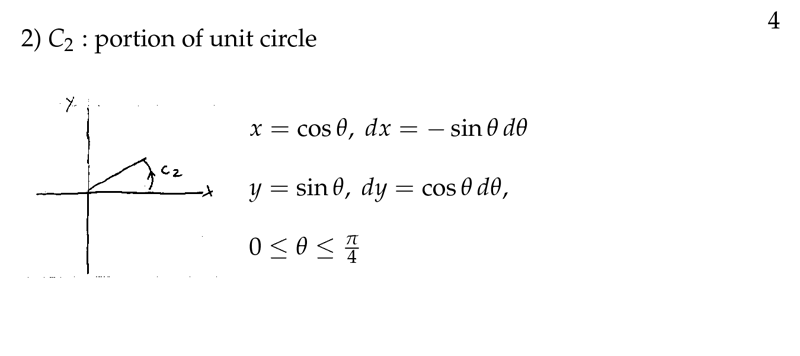
Figure 4: Second trajectory
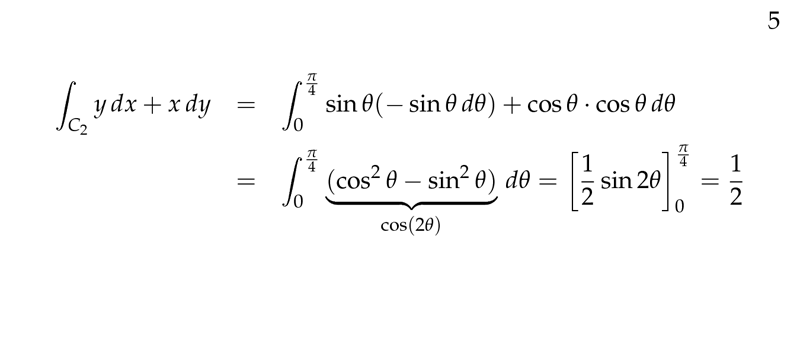
Figure 5: Second trajectory cont
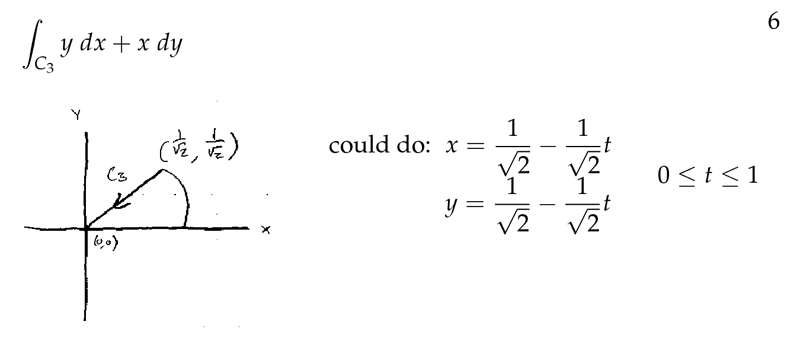
Figure 6: Third trajectory

Figure 7: Third trajectory, better strategy
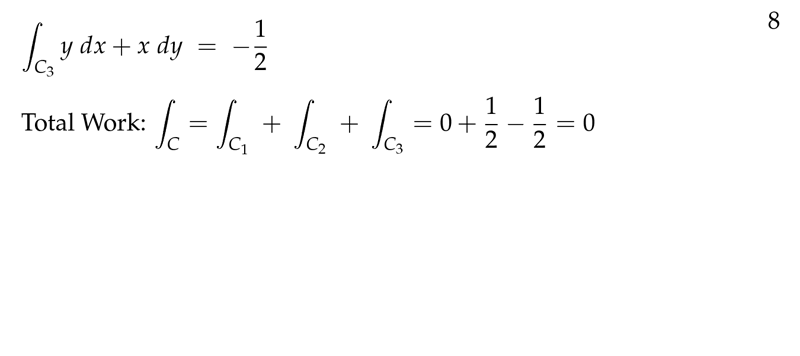
Figure 8: Total work
2 Compute line integral
2.1 Front
Compute line integral
Let \(C\) be the curve \(g(x,y) = x^3y + xy^3 = 5\), \({\displaystyle \int_C \grad{g} \dd{\vb{r}}}\)
2.2 Back
Since \(C\) is a level curve for \(g(x,y)\), we know \(\grad{g} \cdot \dd{\vb{r}} = 0\). Therefore, \({\displaystyle \int_C \grad{g} \dd{\vb{r}} = 0}\)
3 What is a gradient field?
3.1 Front
What is a gradient field?
3.2 Back
It’s a vector fields which define the gradient of \(f(x,y)\) at each point of the field.
Ex: \(\grad{x^3 y^4} = \ev{3x^2y^4, 4x^3y^3}\)
4 How is call \(f\) of this relationship?
4.1 Front
How is call $f$ of this relationship?
\(\grad{f(x,y)} = \ev{f_x, f_y}\), where \(\grad{f}\) is a gradient field
4.2 Back
\(f\) is the potential function