1 Chalkboard
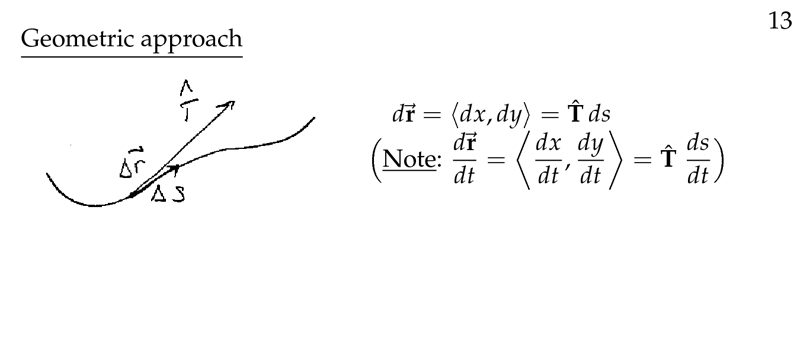
Figure 1: Geometric approach
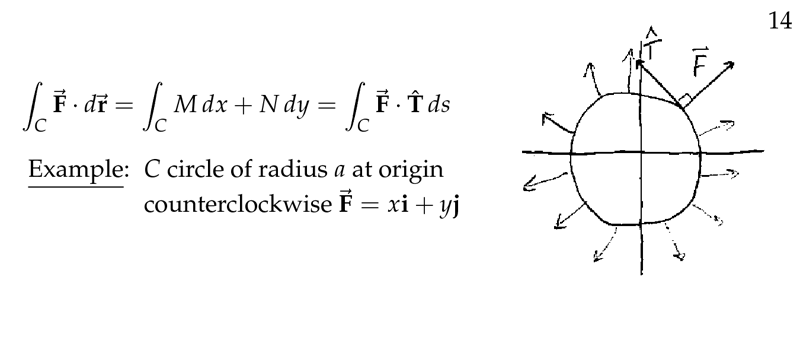
Figure 2: Example \(C\) circle of radius \(a\), and force radially away
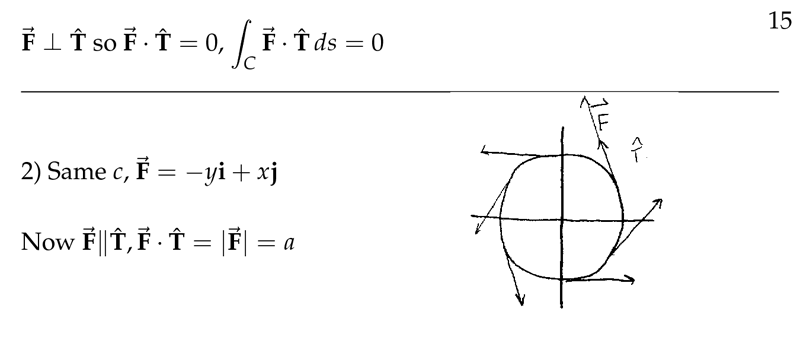
Figure 3: Same \(c\), but force are tanget to the circle
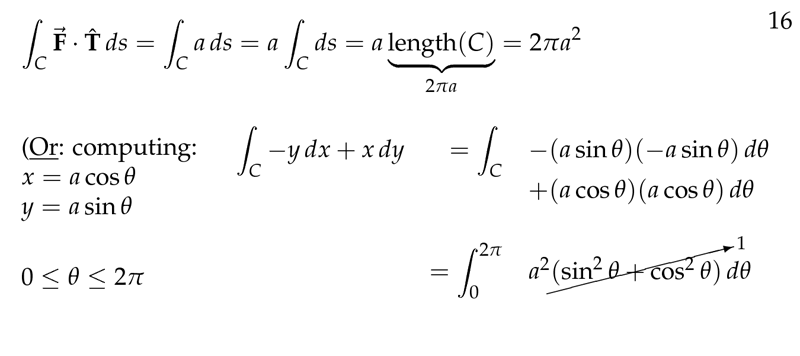
Figure 4: Computing is more long that geometric approach in this case
2 Why is useful to set a geometric graph of line integrals?
2.1 Front
Why is useful to set a geometric graph of line integrals?
2.2 Back
Because sometimes you can avoid the tedious calculations used in computing certain line integrals.
For example, in circle trajectories where force is tangent or radially away from the circle
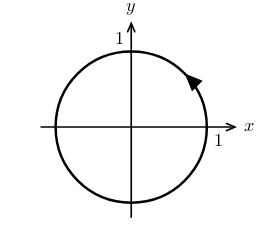
3 How can we write the line integrals in terms of unit tangent vector?
3.1 Front
How can we write the line integrals in terms of unit tangent vector?
\({\displaystyle \int_C \vb{F} \cdot \dd{\vb{r}}}\)
3.2 Back
Recall \({\displaystyle \dv{\vb{r}}{t} = \vb{T} \dv{s}{t}}\), where \(\vb{T}\) is unit tangent, and \(s\) is arc length. So \(\dd{\vb{r} = \vb{T} \dd{s}}\)
Intrinsic formula: \({\displaystyle \int_C \vb{F} \cdot \dd{\vb{r}} = \int_C \vb{F} \cdot \vb{T} \dd{s}}\)
4 Compute this line integral as quick as possible
4.1 Front
Compute this line integral as quick as possible
\({\displaystyle \int_C \vb{F} \cdot \dd{\vb{r}}}\), where \(\vb{F} = \ev{-y, x}\), and \(C\) is the circle with radius \(b\) and traced counterclockwise
4.2 Back
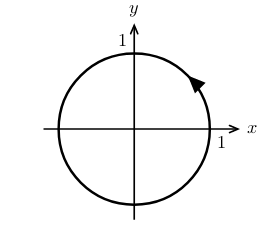
The force field is parallel to the unit tangent vector, so using the intrinsic formula.
\({\displaystyle \int_C \vb{F} \dd{\vb{r}} = \int_C \vb{F}\cdot \vb{T} \dd{s}}\)
Keep in mind, \(x(t) = b \cos(t)\) and \(y(t) = b \sin(t)\)
The tangent vector is \({\displaystyle \vb{T} = \frac{\dd{\vb{r}}}{\abs{\dd{\vb{r}}}} = \ev{-y/b, x/b}}\), so \({\displaystyle \vb{F} \cdot \vb{T} = \frac{y^2 + x^2}{b} = \frac{b^2}{b} = b}\), which is constant
So, \({\displaystyle \int_C \vb{F} \cdot \vb{T} \dd{s} = \int_C b \dd{s} = b \int_C \dd{s} = b 2\pi b = 2 \pi b^2}\)