1 Chalkboard
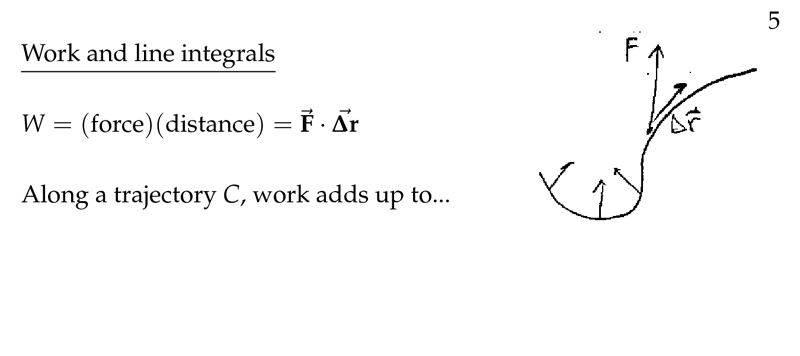
Figure 1: Work and line integrals
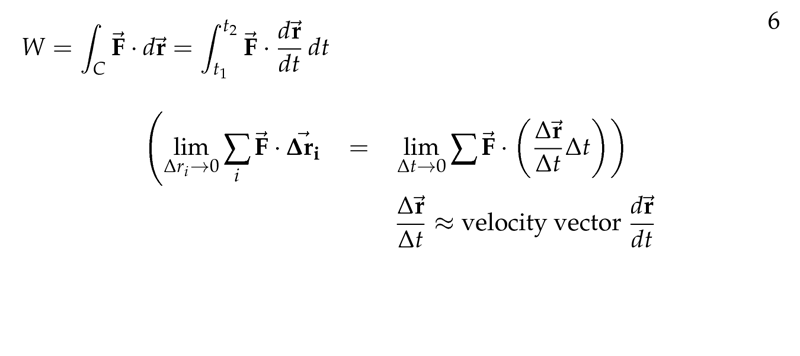
Figure 2: Work as integral
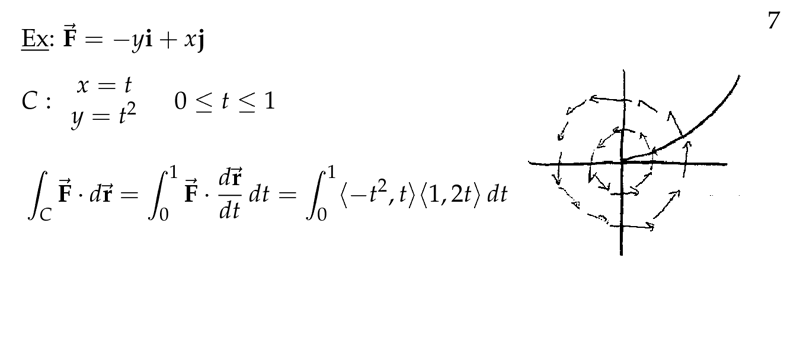
Figure 3: Example of work
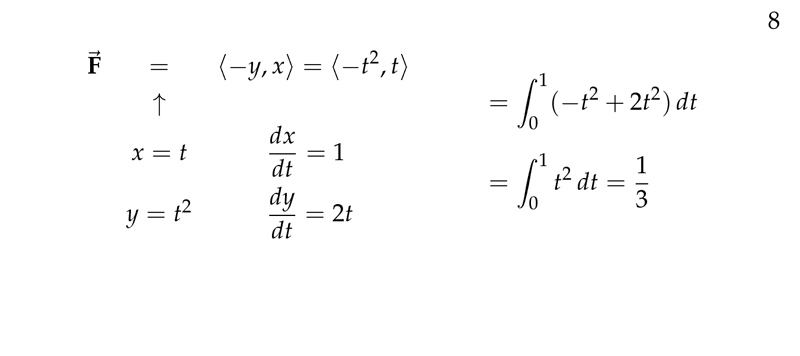
Figure 4: Example cont
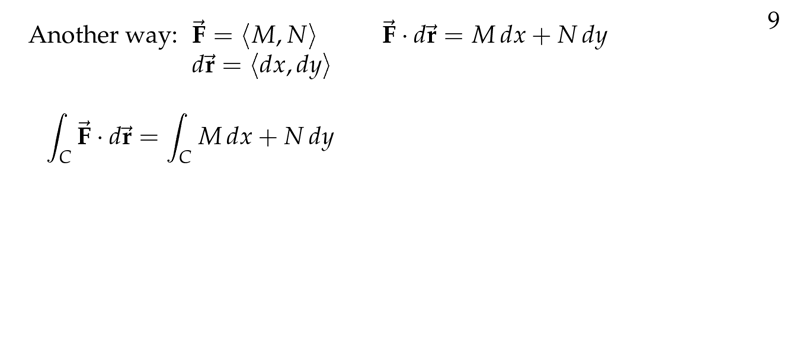
Figure 5: Another way of calculate line integrals
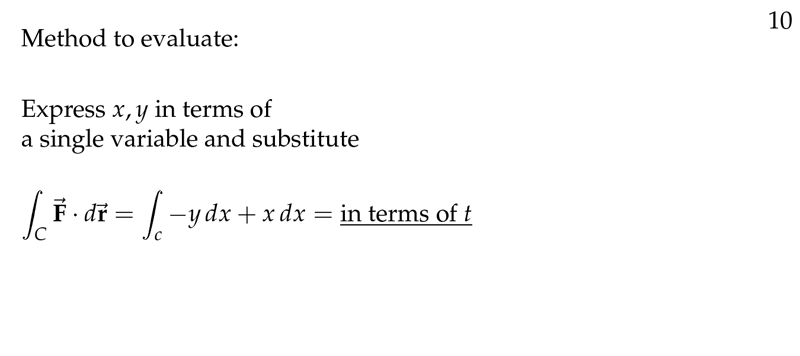
Figure 6: Compute line integrals in terms of one variable
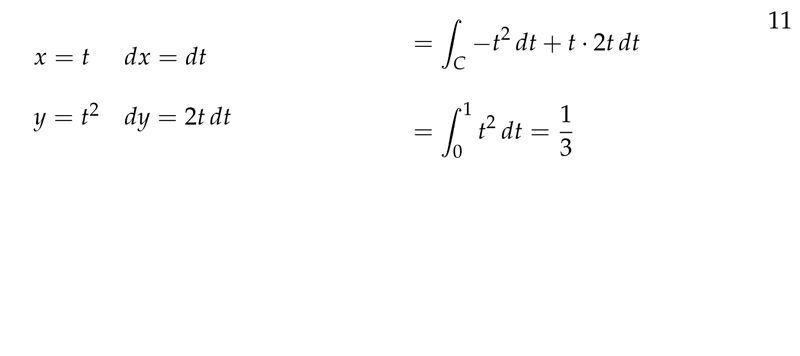
Figure 7: Example

Figure 8: Not practical example
2 How is a line integrals?
2.1 Front
How is a line integrals?
What do you need and notation
2.2 Back
- Field: \(\vb{F} = M \vu{i} + N \vu{j} = \ev{M,N}\)
- Curve: \(\vb{r}(t) = x(t)\vu{i} + y(t)\vu{j} = \ev{x,y} \implies \dd{\vb{r}} = \ev{\dd{x}, \dd{y}}\)
Line integral
\({\displaystyle \int_C \vb{F} \cdot \dd{\vb{r}} = \int_C \ev{M,N} \cdot \ev{\dd{x},\dd{y}} = \int_C M \dd{x} + N \dd{y}}\)
3 How line integrals arise?
3.1 Front
How line integrals arise?
A force \(\vb{F}\) being applied over a displacement \(\vb{\Delta r}\)
Work as line integral
3.2 Back
Work is force times distance, but only the component of the force in the direction of the displacement does any work.
Work = \(\abs{\vb{F}} \cos \theta \abs{\vb{\Delta r}} = \vb{F} \cdot \vb{\Delta r}\)
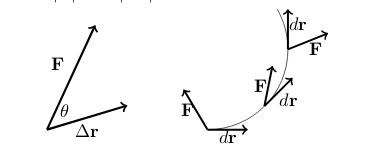
For a variable force applied over a curve the total work is found by “summing” the infinitesimal pieces
Total work is \({\displaystyle \lim_{n \to \infty} \sum_{i=1}^n \vb{F_i} \cdot \Delta \vb{r}}\)
Line integral: \({\displaystyle \int_C \vb{F} \cdot \dd{\vb{r}}}\)
4 How can we compute a line integral?
4.1 Front
How can we compute a line integral?
Using the example: \({\displaystyle I = \int_C x^2 y \dd{x} + (x-2y)\dd{y}}\), over the part of parabola \(y=x^2\) from \((0,0)\) to \((1,1)\)
4.2 Back
- Parametrize the curve
- \(x = t\), \(y = t^2\), \(0 \geq t \geq 1\)
- \(\dd{x} = \dd{t}\), \(\dd{y} = 2t \dd{t}\)
- Substitute everything in the integral
- \({\displaystyle \int_0^1 t^2 (t^2) \dd{t} + (t - 2t^2) 2t \dd{t} = \int_0^1 t^4 + 2t^2 - 4t^3 \dd{t} = - \frac{2}{15}}\)
5 Is the line integral dependent of the parametrization?
5.1 Front
Is the line integral dependent of the parametrization?
Using the same integral, but different parametrization of \(C\), is the line integral different?
5.2 Back
No, the line integral is independent of the parametrization
6 What happens if we reverse the direction of the curve in the line integral?
6.1 Front
What happens if we reverse the direction of the curve in the line integral?
\({\displaystyle \int_{-C} \vb{F} \cdot \dd{\vb{r}}}\)
6.2 Back
The line integral changes sign
\({\displaystyle - \int_C \vb{F} \cdot \dd{\vb{r}}}\)
7 Which notation can we use for closed curve on line integral?
7.1 Front
Which notation can we use for closed curve on line integral?
7.2 Back
\({\displaystyle \oint_C \vb{F} \cdot \dd{\vb{r}}}\)