1 Chalkboard

Figure 1: Vector fields meaning
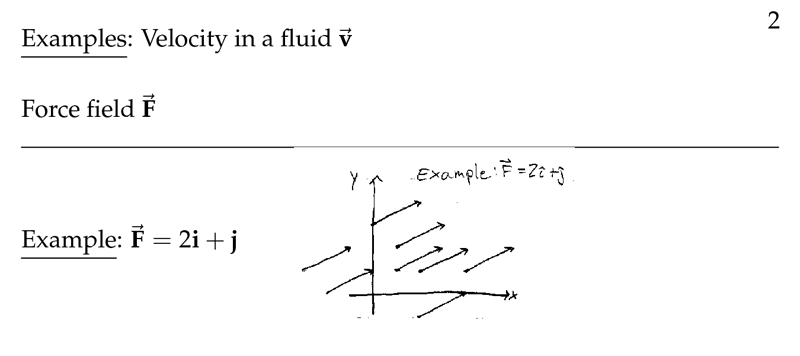
Figure 2: Examples of vector fields (1)
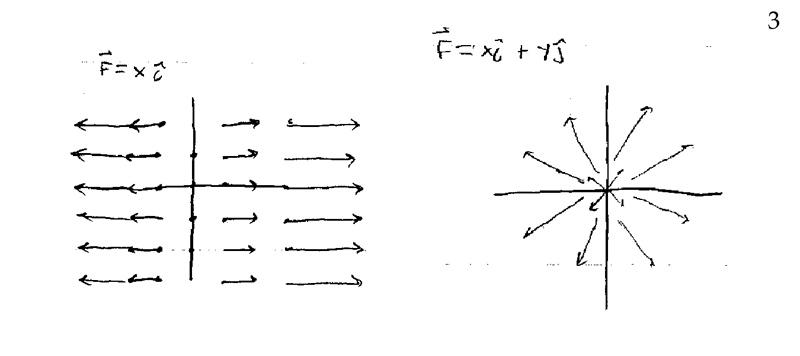
Figure 3: Examples of vector fields (2)
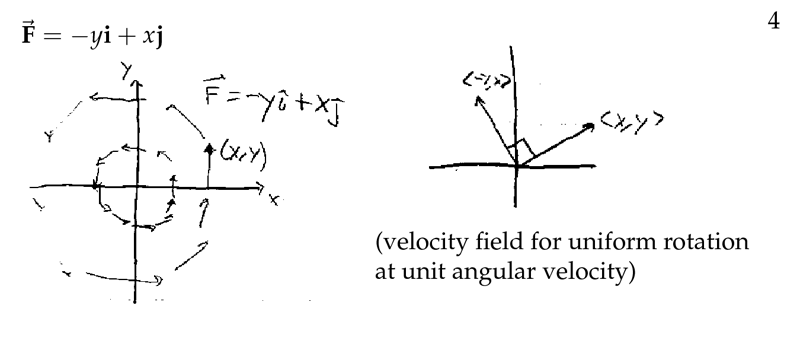
Figure 4: Examples of vector fields (4)
2 How are defined a vector field?
2.1 Front
How are defined a vector field?
2.2 Back
\(\vb{F}(x,y) = M(x,y)\vu{i} + N(x,y)\vu{j}\)
To each pair of values \((x_0,y_0)\) for which both \(M\) and \(N\) are defined, such a function assigns a vector \(\vb{F}(x_0,y_0)\) in the plane.
3 How is called \(\vb{F}\)
3.1 Front
How is called $\vb{F}$
In vector field: \(\vb{F}(x,y) = M(x,y)\vu{i} + N(x,y)\vu{j}\)
3.2 Back
Vector function of two variables
4 Which is the domain of \(\vb{F}\)
4.1 Front
Which is the domain of $\vb{F}$
In vector field
4.2 Back
It’s the set of points \((x,y)\) for which \(\vb{F}\) is defined
5 How can we represent a vector fields?
5.1 Front
How can we represent a vector fields?
\(\vb{F}(x,y) = M(x,y)\vu{i} + N(x,y)\vu{j}\)
5.2 Back
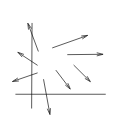
At each point \((x_0, y_0)\) in the domain we place the corresponding vector \(\vb{F}(x_0,y_0)\) so that its tail is at \((x_0,y_0)\)
6 Which differences are there between vector field and vector function?
6.1 Front
Which differences are there between vector field and vector function?
In a region of \(xy\text{-plane}\)
6.2 Back
There is no real distinction between them. Usually in physics, we will use the same symbol \(\vb{F}\) to denote both the field and the functions. Saying “the vector field \(\vb{F}\)”, rather than “the vector field corresponding to the vector function \(\vb{F}\)”
7 When can we say that the vector field \(\vb{F}\) is continuous?
7.1 Front
When can we say that the vector field $\vb{F}$ is continuous?
In some region, \(\vb{F}(x,y) = M(x,y)\vu{i} + N(x,y)\vu{j}\)
7.2 Back
If \(M(x,y)\) and \(N(x,y)\) are continuous functions in that region.
As you move around the field, the vectors should change direction and magnitude smoothly, without sudden jumps in size or direction
8 When can we say that the vector field \(\vb{F}\) is differentiable?
8.1 Front
When can we say that the vector field $\vb{F}$ is differentiable?
In some region, \(\vb{F}(x,y) = M(x,y)\vu{i} + N(x,y)\vu{j}\)
8.2 Back
When in this region, \(M(x,y)\) and \(N(x,y)\) are differentiable, that is, if all the partial derivatives (\(\pdv{M}{x}\), \(\pdv{M}{y}\), \(\pdv{N}{x}\), \(\pdv{N}{y}\)) exists in the region.
If the partial derivatives are continuous in this region, we can say that \(\vb{F}\) is continuously differentiable
9 What is a gradient vector field?
9.1 Front
What is a gradient vector field?
\(w = f(x,y)\)
9.2 Back
If \(f(x,y)\) is a differentiable function of 2 variables, its gradient
\({\displaystyle \grad{w} = \pdv{w}{x} \vu{i} + \pdv{w}{y} \vu{j}}\)
Where the direction of \(\grad{w}\) is the direction of \(\vu{u}\) in which \({\displaystyle \eval{\dv{w}{s}}_{\vu{u}}}\) is greatest, and its modules is \({\displaystyle \eval{\dv{w}{s}}_{\vu{u}}}\),
10 How is a gradient field of \(f\) at contour curves?
10.1 Front
How is a gradient field of $f$ at contour curves?
At \(f(x,y) = c\)
10.2 Back
\(\grad{w}\) is perpendicular to the contour curves of \(f(x,y)\)
11 What is a force field?
11.1 Front
What is a force field?
Example: two-dimensional electrostatic force field, and gravitational force (in the \(xy\text{-plane}\))
11.2 Back
At each point \((x_0,y_0)\) of the plane, we put a vector representing the force.
For the two dimensional electrostatic force field each force vector would act on a unit positive charge placed at that point
In the gravitational field, the gravitational force acting at each point on a unit mass.
12 What is a two-dimensional steady-state flow?
12.1 Front
What is a two-dimensional steady-state flow?
And, describe their vector fields
12.2 Back
It’s a fluid flowing in a horizontal shallow tank of uniform depth, and assume that the flow pattern at any point is purely horizontal and not changing with time.
The fluid can either be compressible (like a gas) or incompressible (like water).
The fluid is being added to or subtracted from the flow (pouring water)
2 vector fields
- Velocity field \(\vb{v}(x,y)\) where the vector \(\vb{v}\) at the point \((x,y)\) represents the velocity vector of the flow at that point. With direction of the flow and magnitude gives the speed of the flow
- Flow field: \(F = \delta(x,y) \vb{v}(x,y)\), where \(\delta(x,y)\) gives the density of the fluid at the point \((x,y)\) in terms of mass per unit area.
13 How is defined the flow field?
13.1 Front
How is defined the flow field?
\(\vb{F} = \delta(x,y) \vb{v}(x,y)\)
13.2 Back
- \(\vb{v}(x,y)\) is the velocity field
- \(\delta(x,y)\) is the density of the fluid at point (x,y)
\(\vb{F}(x,y)\) (assuming it no 0 at a point \((x,y)\))
- dir \(\vb{F}\) = direction of fluid flow at \((x,y)\)
- \(\abs{\vb{F}}\)
- rate (per unit length per second) of mass transport
- across a line perpendicular to the flow direction at \((x,y)\)
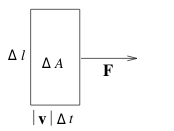
, \({\displaystyle \abs{\vb{F}} \Delta l \Delta t = \delta \abs{\vb{v}} \Delta t \Delta l}\) = mass in \(\Delta A\). If we dividing by \(\Delta l \Delta t\) and letting \(\Delta l\) and \(\Delta t \to 0\), \(\vb{F} = \delta(x,y) \vb{v}(x,y)\)
If density \(\delta_0\) is constant, it would be for an incompressible fluid at a uniform temperature, then the flow field and velocity field are essentially the same.
14 Sketch vector field of Force, constant gravitational field
14.1 Front
Sketch vector field of Force, constant gravitational field
\(\vb{F}(x,y) = -g \vu{j}\)
14.2 Back
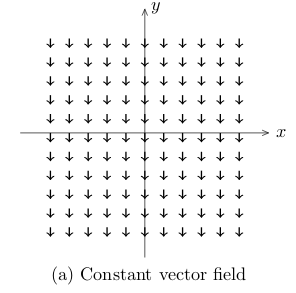
15 Sketch vector field of velocity shrinking radial field
15.1 Front
Sketch vector field of velocity shrinking radial field
\(\vb{V}(x,y) = \ev{x,y}/r^2\), for example water pouring from a source at \((0,0)\)
15.2 Back
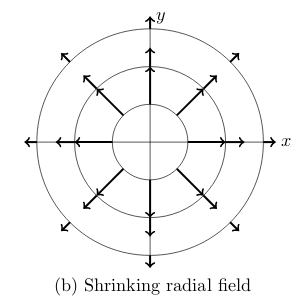
16 Sketch vector field of unit tangential field
16.1 Front
Sketch vector field of unit tangential field
\(\vb{F} = \ev{-y,x} / r\)
16.2 Back
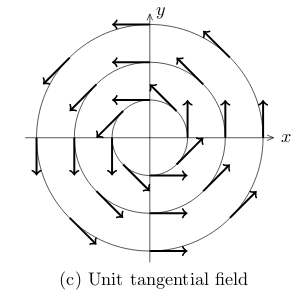
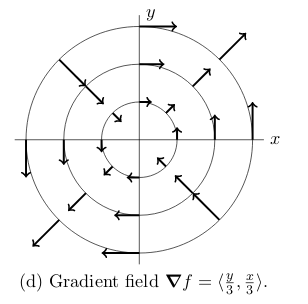
17 Sketch vector field of a gradient
17.1 Front
Sketch vector field of a gradient
\(\vb{F} = \grad{f}\), where \({\displaystyle f(x,y) = \frac{xy}{3}}\) and \(\grad{f} = \ev{\frac{y}{3}, \frac{x}{3}}\)
17.2 Back