1 Chalkboard
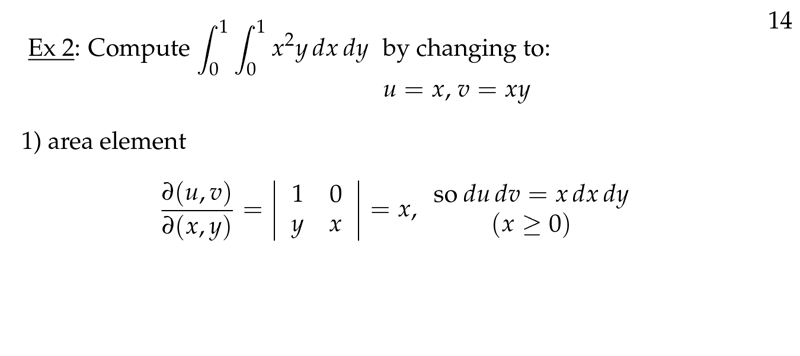
Figure 1: Area element
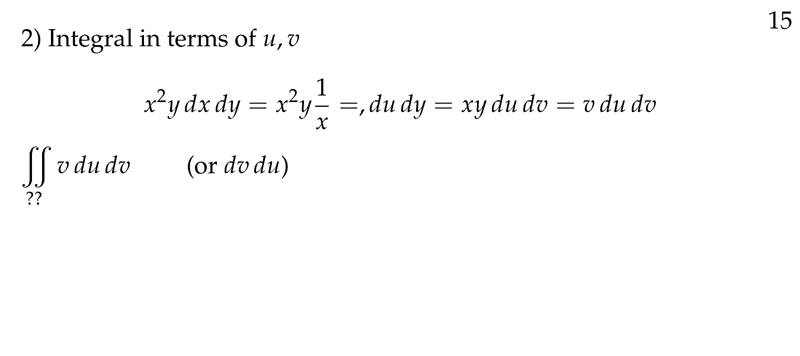
Figure 2: Integrand in terms of \(u,v\)
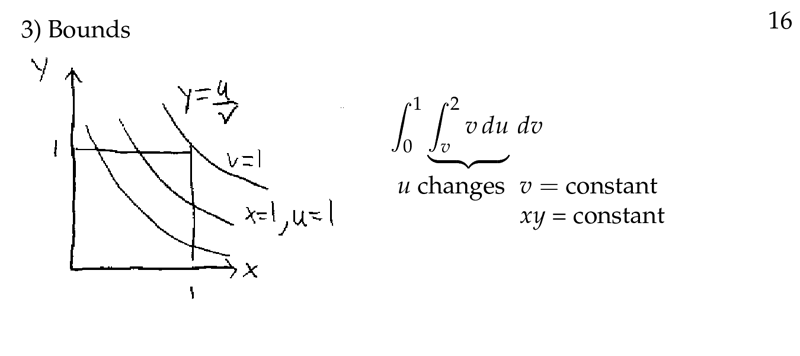
Figure 3: Bounds
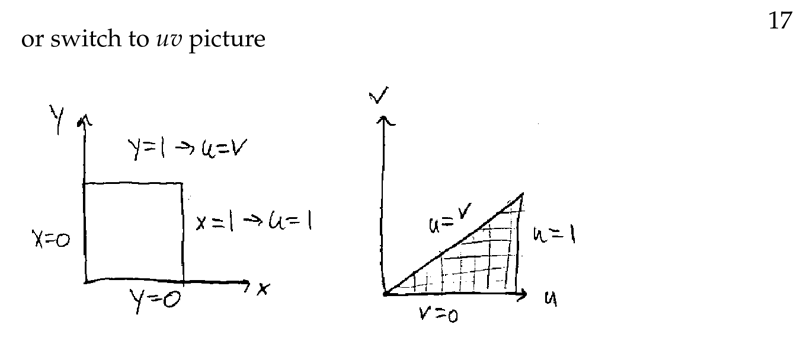
Figure 4: Bounds switching to \(uv\) picture
2 How can we compute \(\Delta A\) in another \(u,v\) coordinates
2.1 Front
How can we compute $\Delta A$ in another $u,v$ coordinates
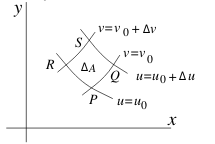
Proof of the Jacobian Formula and get \(\dd{A}\) too
2.2 Back
\(\Delta A \approx \qq{area of parallelogram PQRS} = \abs{PQ \cross PR}\)
In \(u,v\) system, the points
- \(P = (u_0, v_0)\)
- \(Q = (u_0 + \Delta u, v_0)\)
- \(R = (u_0, v_0 + \Delta v)\)
\(PQ\) and \(PR\) in \(\vu{i}\), \(\vu{j}\) coordinates. Consider first \(PQ\)
- \(PQ = \Delta x \vu{i} + \Delta y \vu{j}\)
- Hold \(v = v_0\) and change \(u_0 \to u_0 + \Delta u\)
- \({\displaystyle \Delta x \approx \biggl(\pdv{x}{u} \biggr)_0 \Delta u}\)
- \({\displaystyle \Delta y \approx \biggl(\pdv{y}{u} \biggr)_0 \Delta u}\)
- \({\displaystyle PQ \approx \biggl(\pdv{x}{u} \biggr)_0 \Delta u \vu{i} + \biggl(\pdv{y}{u} \biggr)_0 \Delta u \vu{j}}\)
As same way, hold \(u = u_0\) and increasing \(v_0\) by \(\Delta v\)
- \({\displaystyle PR \approx \biggl(\pdv{x}{v} \biggr)_0 \Delta v \vu{i} + \biggl(\pdv{y}{v} \biggr)_0 \Delta v \vu{j}}\)
Since vectors are in the \(xy\text{-plane}\), \(PQ \cross PR\) has only a \(\vu{k}\) component.
- \(\vu{k}\) component of \(PQ \cross PR \approx \begin{vmatrix} x_u \Delta u & y_u \Delta u \ x_v \Delta v & y_v \Delta v \end{vmatrix}_0 = \begin{vmatrix} x_u & x_v \ y_u & y_v \end{vmatrix}_0 \Delta u \Delta v\)
First taking the transpose (which doesn’t change its value), then factored the \(\Delta u\) and \(\Delta v\) out of the two columns. Taking the absolute value, the definition of Jacobian is
\({\displaystyle \Delta A \approx \abs{PQ \cross PR} = \abs{\pdv{(x,y)}{(u,v)}}_0 \Delta u \Delta v}\)
As \(\Delta u, \Delta v \to 0\), dropping subscript \(0\) (so that \(P\) becomes any point in the plane)
\(\dd{A} = \abs{\pdv{(x,y)}{(u,v)} \dd{u} \dd{v}}\)
3 How can we integrate this function?
3.1 Front
How can we integrate this function?
\({\displaystyle \int_{-\infty}^{\infty} e^{-x^2} \dd{x}}\)
3.2 Back
Steps:
- Set as double integral
- Change to polar coordinate
- Compute the double integral
- Get single integral value
Calculation:
- We call \({\displaystyle I = \int_{-\infty}^{\infty} e^{-x^2} \dd{x}}\)
- We will use double integral, as this
- \({\displaystyle \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2 -y^2} \dd{x} \dd{y}}\)
- In the inner integral \(e^{-y^2}\) is constant, so we can write as \({\displaystyle \int_{-\infty}^{\infty} e^{-y^2} \int_{-\infty}^{\infty} e^{-x^2} dx dy}\)
- After getting inner integral, we will get another constant, specifically \({\displaystyle I = \int_{-\infty}^{\infty} e^{-x^2} \dd{x}}\)
- \({\displaystyle I \int_{-\infty}^{\infty} e^{-y^2} \dd{y} = I^2}\)
Now, we can calculate \(I^2\) and \(I = \sqrt{I^2}\). We calculate this double integral using polar coordinates
\({\displaystyle I^2 = \int_0^{\infty} \int_0^{2\pi} e^{- r^2} r \dd{r} \dd{\theta} = 2 \pi \int_0^{\infty} e^{-r^2} r \dd{r} = 2\pi (- \frac{e^{-r^2}}{2}) \bigg|_0^{\infty} = 0 - 2\pi \frac{-1}{2} = \pi}\)
\(I = \sqrt{\pi}\)
4 Is it necessary to get inverse equations for calculate the Jacobian?
4.1 Front
Is it necessary to get inverse equations for calculate the Jacobian?
On changing variables in Multiple Integrals
4.2 Back
No, you don’t need to. Both Jacobian are reciprocal
\({\displaystyle \pdv{(x,y)}{(u,v)} \pdv{(u,v)}{(x,y)} = 1}\)
You can calculate the easiest Jacobian, and then get the inverse
5 Suggest a change of variable for evaluate this integral
5.1 Front
Suggest a change of variable for evaluate this integral
\({\displaystyle \iint_R \frac{y}{x} \dd{x} \dd{y}}\)
Bounded by the curves, \(x^2 - y^2 = 1\), \(x^2 - y^2 = 4\), \(y=0\), \(y = x/2\)
5.2 Back
Looking at boundaries and integrand we can suggest the changes of variable
\({\displaystyle u = x^2 - y^2}\) and \({\displaystyle v = \frac{y}{x}}\)
Then, you can get the Jacobian \({\displaystyle \pdv{(u,v)}{(x,y)}}\) and get the reciprocal for changing variables.
6 Where can we find problems setting the limit of region on changing variables?
6.1 Front
Where can we find problems setting the limit of region on changing variables?
For example, changing \(u = x+y\), \(v = x-y\) on \({\displaystyle \int_0^1 \int_0^x \dd{y}\dd{x}}\)
6.2 Back
In this example, the region is not bounded by contour curves, so we need to figure out the \(uv-\text{equations}\) of the boundary curves.
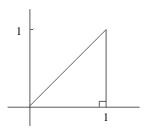
- Diagonal boundary, is the contour curve \(v=0\)
- Horizontal and vertical boundaries are not contour curves, what are their \(uv-\text{equations}?\)
Method 1: Eliminate \(x\) and \(y\) from the equations
- \(u = u(x,y) = x + y\)
- \(v = v(x,y) = x - y\)
- \(xy-\text{equation}\) of the boundary curve (\(y=0\), and \(x=1\))
For \(x-axis\), \(y=0 \implies u=v\)
For \(x=1\), \(u + v = 2\)
7 How can we set a coordinate system for calculate moment of inertia?
7.1 Front
How can we set a coordinate system for calculate moment of inertia?
- Moment of inertia about the hypotenuse of a right triangle with leg \(a\) and density \(\delta(x,y) = 1\)
Set the figure a good placement in the coordinate system, and set-up the integral
7.2 Back
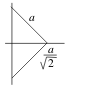
\({\displaystyle \int_0^{a/\sqrt{2}} \int_{x - a/\sqrt{2}}^{a/\sqrt{2} -x} x^2 \dd{y}\dd{x}}\)
8 How can we set a coordinate system for calculate center of gravity?
8.1 Front
How can we set a coordinate system for calculate center of gravity?
- Center of gravity of a sector of a circular disc of radius \(a\) which vertex angle if “2α”
8.2 Back
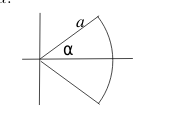
By symmetry \(\overline{y}\) lies on the \(x\text{-axis}\)
Calculate \({\displaystyle \overline{x} = 2 \int_0^{\alpha} \int_0^a r \cos \theta r \dd{r} \dd{\theta}}\)
Result: \({\displaystyle \overline{x} = \frac{2a \sin \alpha}{3 \alpha}}\)