1 Chalkboard
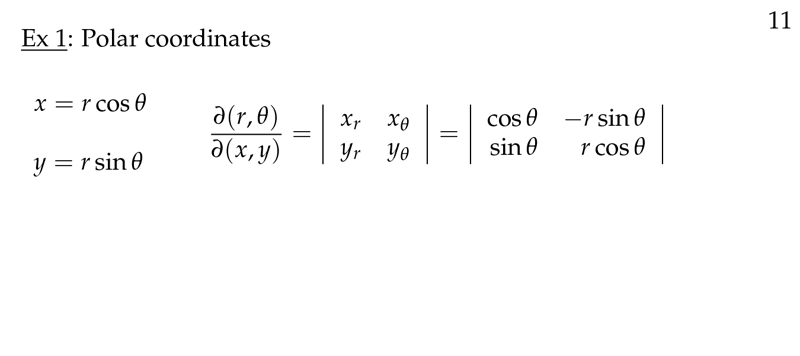
Figure 1: Polar coordinates
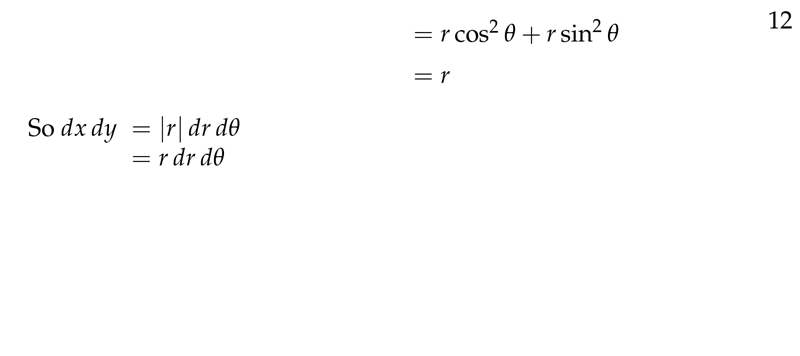
Figure 2: Scaling factor
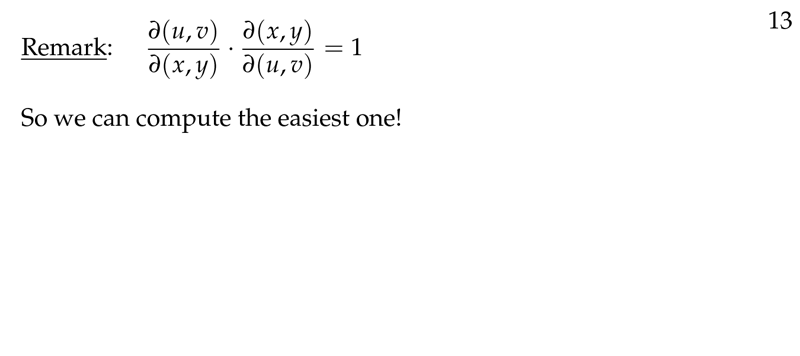
Figure 3: Recall reciprocal rule for partial derivatives
2 Proof \(dA\) in polar coordinates with the Jacobian
2.1 Front
Proof $\dd{A}$ in polar coordinates with the Jacobian
\(\dd{A} = r \dd{r} \dd{\theta}\)
2.2 Back
- \(x = r \cos \theta\)
- \(y = r \sin \theta\)
- \(\dd{A} = \pdv{(x,y)}{(r,\theta)} \dd{r} \dd{\theta}\)
\({\displaystyle \pdv{(x,y)}{(r,\theta)} = \begin{vmatrix} x_r & x_{\theta} \ y_r & y_{\theta} \end{vmatrix} = \begin{vmatrix} \cos \theta & -r \sin \theta \ \sin \theta & r \cos \theta \end{vmatrix} = r (\cos^2 \theta + \sin^2 \theta) = r}\)
So, \(\dd{A} = r \dd{r} \dd{\theta}\)
We can omit the absolute value, since by convention, in integration problems we always assume \(r \geq 0\), as is implied already by the equations
3 How do we get the area element for any \(u,v\) coordinates?
3.1 Front
How do we get the area element for any $u,v$ coordinates?
Explain it briefly, and geometrically
3.2 Back
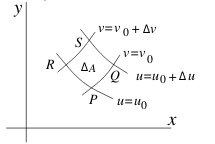
The grid curves divide up the plane into small regions \(\Delta A\) bounded by these contour curves.
If the contour curves are close together, they will be approximately parallel, so that the grid element will be approximately a small parallelogram.