1 Chalkboard

Figure 1: Change variable in double integral
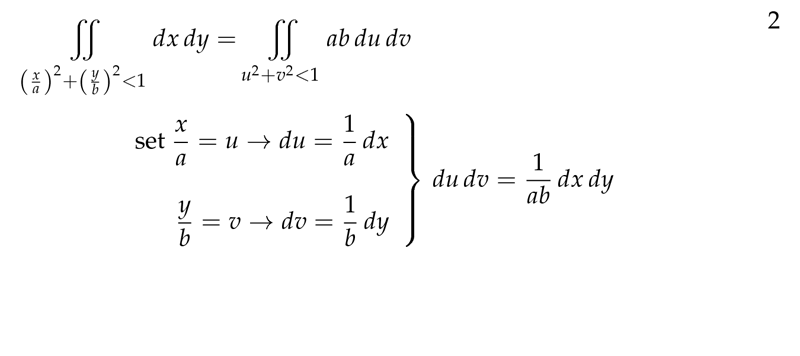
Figure 2: Basic example
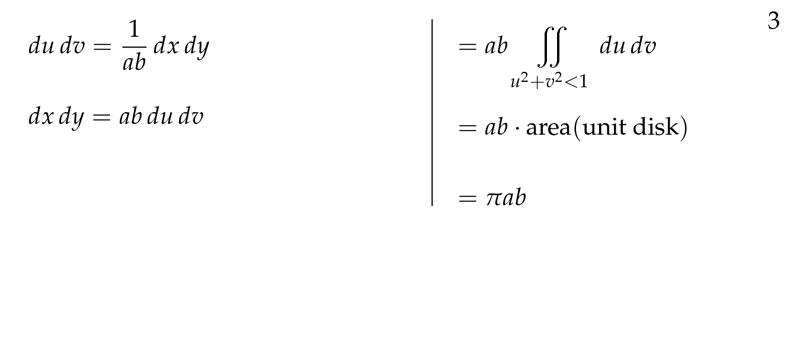
Figure 3: Basic example continuation
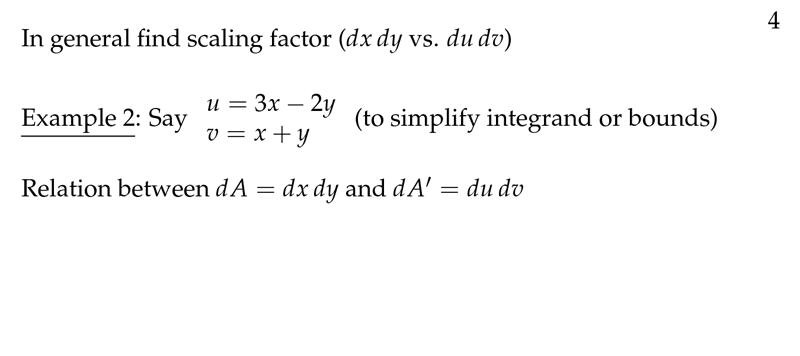
Figure 4: Find scaling factor

Figure 5: Linear change of variables
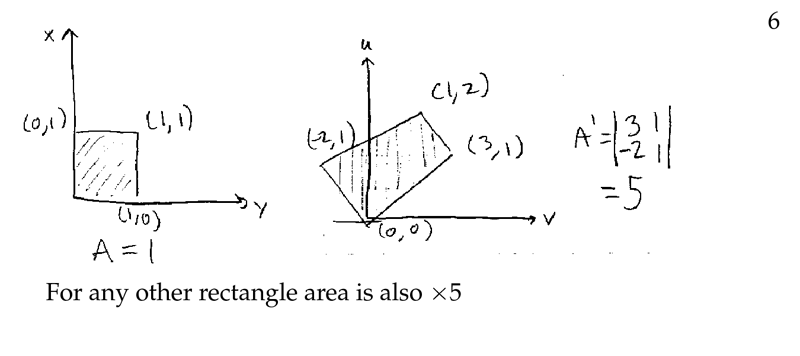
Figure 6: Example of linear change of variable
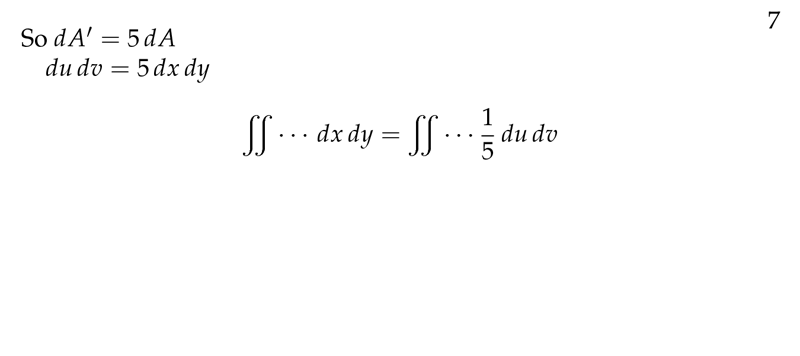
Figure 7: Example: factor scaling
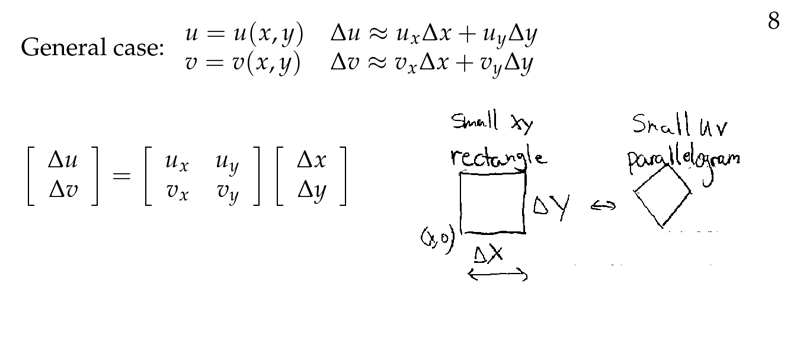
Figure 8: General case
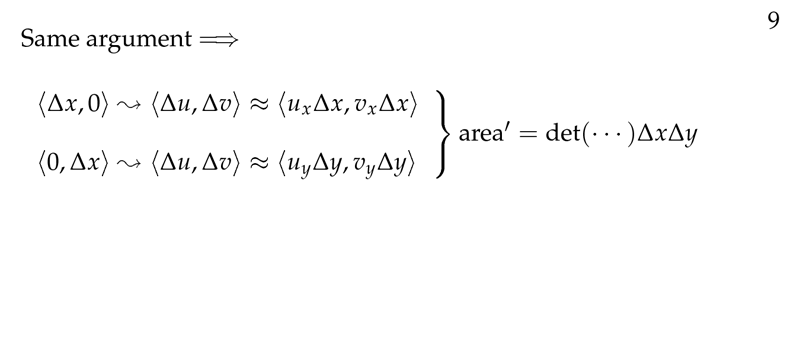
Figure 9: General case 2
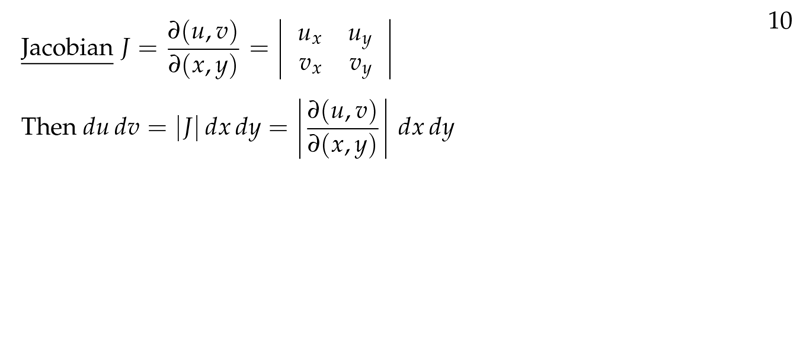
Figure 10: Jacobian as determinant of partial derivatives
2 Why is useful changing the coordinate system in double integrals?
2.1 Front
Why is useful changing the coordinate system in double integrals?
2.2 Back
Because a one better coordinate system is more adapted to the region or integrand than Cartesian coordinate system \((x,y)\)
3 What step do we need for change a double integral in polar coordinates?
3.1 Front
What step do we need for change a double integral in polar coordinates?
For example: polar coordinates
\({\displaystyle \iint_R f(x,y) \dd{A}}\)
3.2 Back
- Changing the integrand \(f(x,y)\) to \(g(r,\theta)\)
- \(r = \sqrt{x^2 + y^2}\)
- \(\theta = \arctan(y/x)\)
- \(x = r \cos \theta\)
- \(y = r \sin \theta\)
- Supplying the area element in the \(r,\theta\) system: \(\dd{A} = r \dd{r} \dd{\theta}\)
- Using the region \(R\) to determine the limits of integration in the \(r, \theta\) system.
4 How can we get the area element in another coordinate system?
4.1 Front
How can we get the area element in another coordinate system?
- \(u(x,y)\)
- \(v(x,y)\)
4.2 Back
Using a determinant called the Jacobian
\({\displaystyle \pdv{(x,y)}{(u,v)} = \begin{vmatrix} x_u & x_v \ y_u & y_v \end{vmatrix}}\)
The formula for the area element in the \(u,v\) system is
\({\displaystyle \dd{A} = \abs{\pdv{(x,y)}{(u,v)}} \dd{u} \dd{v}}\)
5 What is the formula of change variable for a double integral?
5.1 Front
What is the formula of change variable for a double integral?
\({\displaystyle \iint_R f(x,y) \dd{x} \dd{y}}\)
5.2 Back
\({\displaystyle \iint_R f(x,y) \dd{x}\dd{y} = \iint_R g(u,v) \abs{\pdv{(x,y)}{(u,v)}} \dd{u} \dd{v}}\)
Where \(g(u,v)\) is getting from substitution