1 Chalkboard
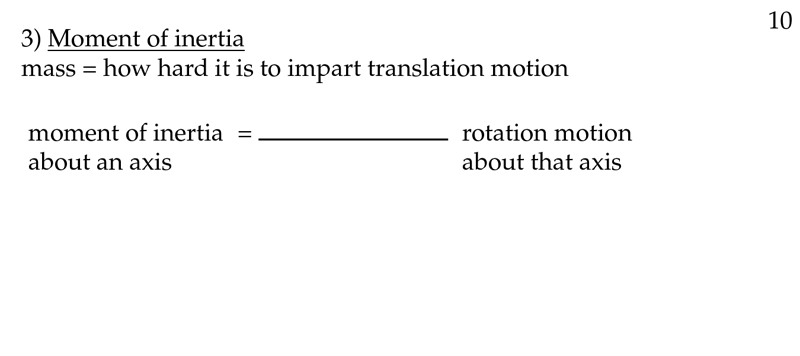
Figure 1: Moment of inertia
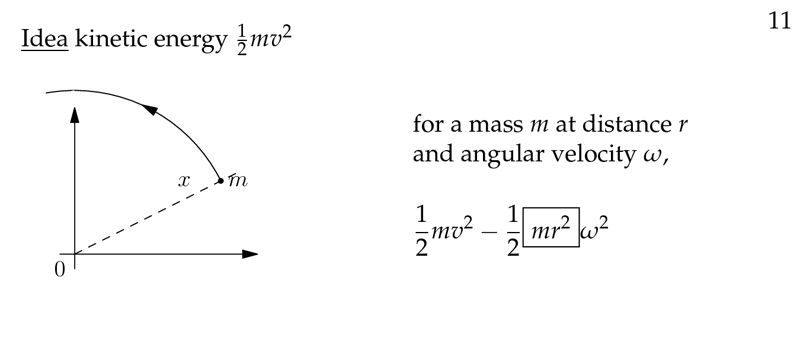
Figure 2: Kinetic energy

Figure 3: Moment of inertia for each \(\Delta A\)
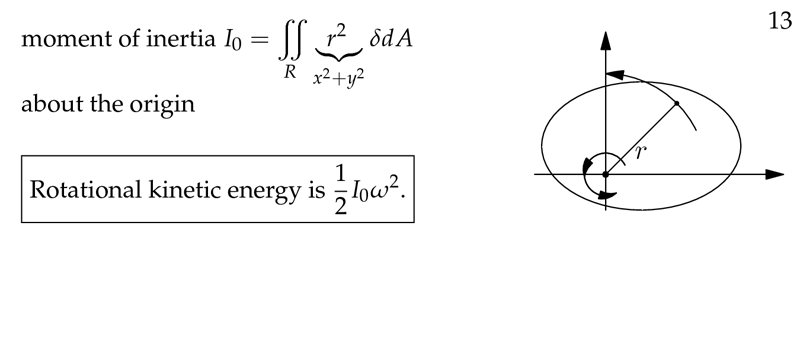
Figure 4: Moment of inertia about the origin
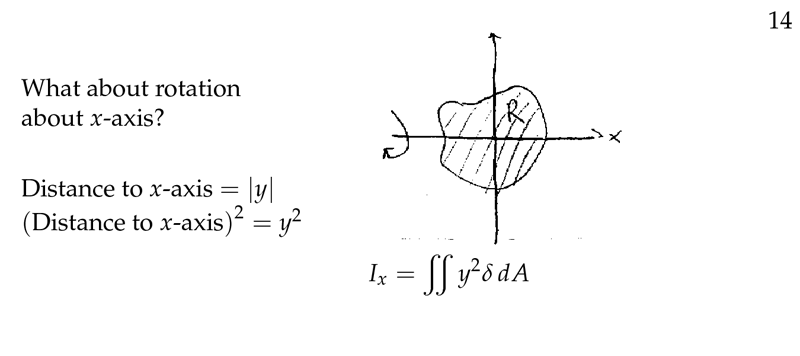
Figure 5: Moment of inertia about \(x\text{-axis}\)
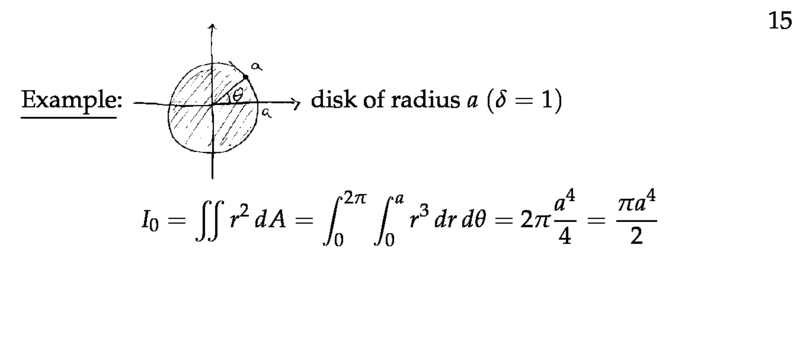
Figure 6: Example of moment of inertia
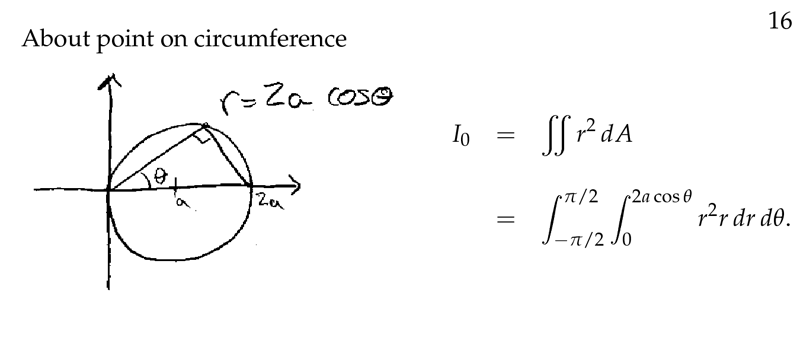
Figure 7: Moment of inertia in a point of the circumference
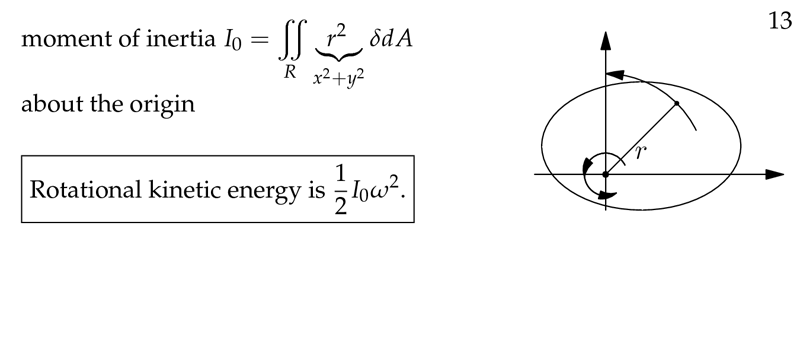
Figure 8: Rotational kinetic energy
2 What is the moment of inertia equation?
2.1 Front
What is the moment of inertia equation?
2.2 Back
\(I = m r^2\), where \(r\) is the distance from the mass to the rotation axis
3 What is the moment of inertia?
3.1 Front
What is the moment of inertia?
Describe it briefly
3.2 Back
It measures an object’s resistance (inertia) to a change in its rotational motion. It is analogous to the way mass measure the resistance to changes in the object’s linear motion.
Is always measured about a reference line, which is though of as the axis of rotation
4 What is the axis of rotation?
4.1 Front
What is the axis of rotation?
Describe it briefly
4.2 Back
It’s the reference line used to measured the moment of inertia. For example, is \(d\) is the distance from the mass to this line
\(I = md^2\)
5 Which is the moment of inertia for each piece?
5.1 Front
Which is the moment of inertia for each piece?
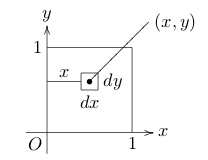
Moment of inertia about the \(y\text{-axis}\)
- Density: \(\delta(x,y) = xy\)
5.2 Back
- Distance for each piece to \(y\text{-axis} = x\)
- Mass of each piece: \(dm = \delta(x,y) dA\)
\(dI = r^2 dm = x^2 \delta(x,y)dA = x^3y dA\)
6 Where is from the equation of moment of inertia?
6.1 Front
Where is from the equation of moment of inertia?
6.2 Back
- Kinetic energy: \({\displaystyle E = \frac{1}{2}mv^2}\)
- Relation between rotation speed and linear speed
- \(v = rw\), where \(r\) is the distance from the axis of rotation, \(w\) it’s angular velocity
It’s from the rotational kinetic energy: \({\displaystyle E = \frac{1}{2}mv^{2} = \frac{1}{2}m r^2 w^2}\)
\(I = mr^2\)
7 What is the polar moment of inertia?
7.1 Front
What is the polar moment of inertia?
Of a planar region
7.2 Back
The polar moment of inertia of a planar region is the moment of inertia about the origin.
The axis of rotation is the \(z\text{-axis}\)