1 Chalkboard
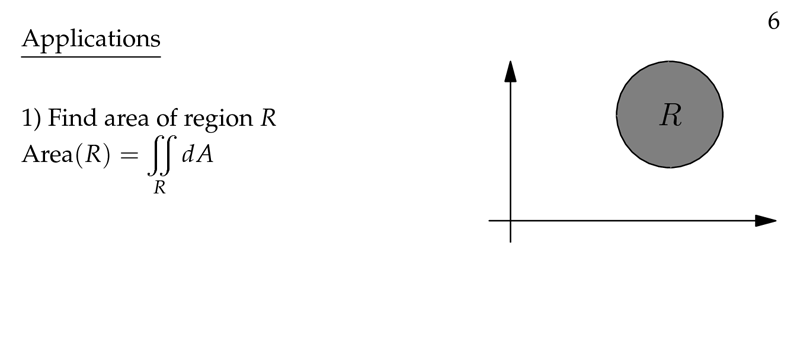
Figure 1: Area of a region \(R\)

Figure 2: Mass of a flat object with density \(\delta\)
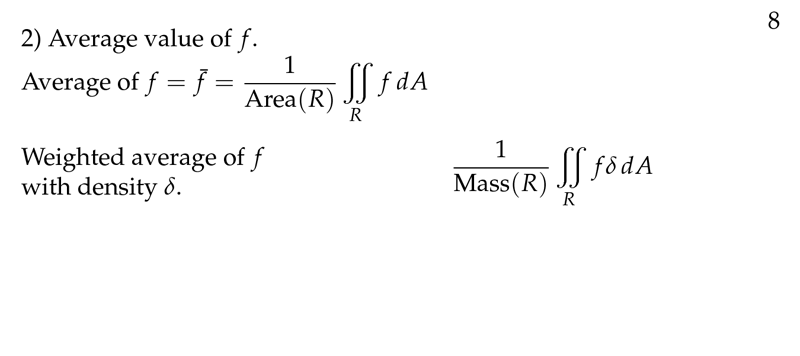
Figure 3: Average value of \(f\)
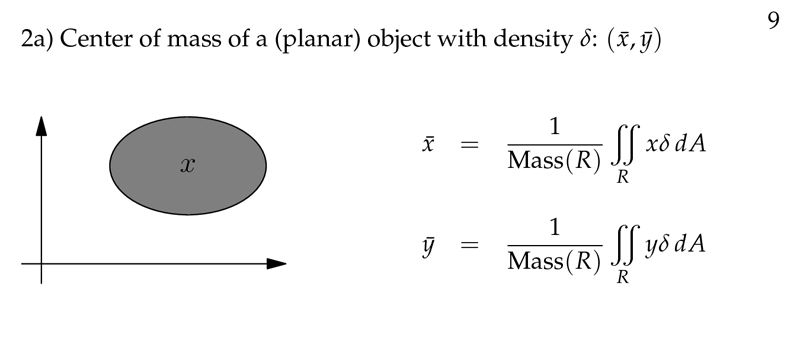
Figure 4: Center of mass of a (planar) object with density \(\delta\)
2 What is the center of mass of a planar object?
2.1 Front
What is the center of mass of a planar object?
- Planar object delimited by \(R\)
- Density area, \(\delta(x,y)\)
2.2 Back
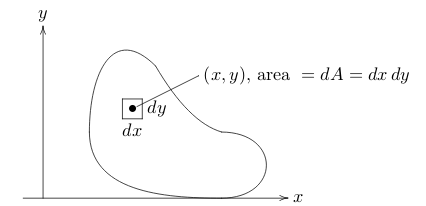
- Dividing the object in small area (infinitesimally), the mass of the area is \(\delta(x,y) \dd{A}\)
- Total mass is: \({\displaystyle M = \iint_R \delta(x,y) \dd{A}}\)
Likewise the \(x\) and \(y\) coordinates of the center of mass are just the weighted average of the \(x\) and \(y\) coordinates of each of the pieces. Center of mass is the point \((\overline{x}, \overline{y})\)
- \({\displaystyle \overline{x} = \frac{1}{M} \iint_R x \delta(x,y) \dd{A}}\)
- \({\displaystyle \overline{y} = \frac{1}{M} \iint_R y \delta(x,y) \dd{A}}\)
3 Define with words what is the center of mass?
3.1 Front
Define with words what is the center of mass?
3.2 Back
Is the weighted average position of the mass, where mass is the product of density and area.
4 Which is the average value of \(f(x,y)\) with respect to area on a region \(R\)?
4.1 Front
Which is the average value of $f(x,y)$ with respect to area on a region $R$?
4.2 Back
\({\displaystyle \text{Average of f} = \overline{f} = \frac{1}{\text{Area(R)}} \iint_R f(x,y) \dd{A}}\)
Where \({\displaystyle \text{Area(R)} = \iint_R \dd{A}}\)
5 What is the geometric center?
5.1 Front
What is the geometric center?
5.2 Back
Is the point given by the average value of \(x\) and \(y\) with respect to area
6 When we can say that the center of mass is equal to the geometric center?
6.1 Front
When we can say that the center of mass is equal to the geometric center?
6.2 Back
When density function is \(\delta=1\)