1 Chalkboard
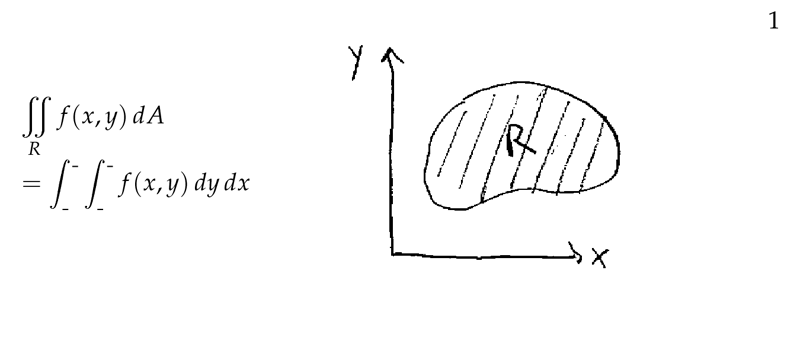
Figure 1: Double integral as interated integral \(\dd{y}\dd{x}\)
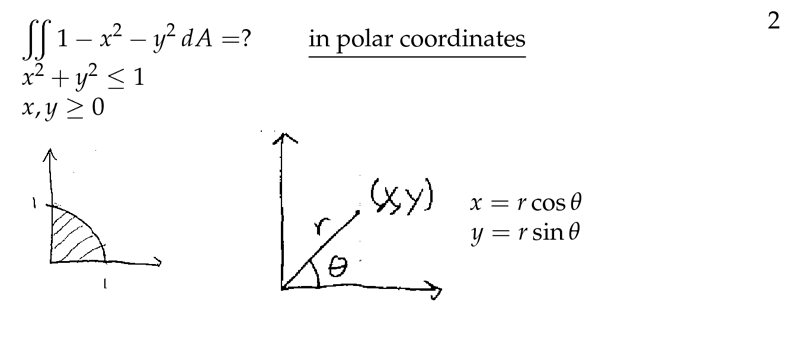
Figure 2: Function in polar coordinates
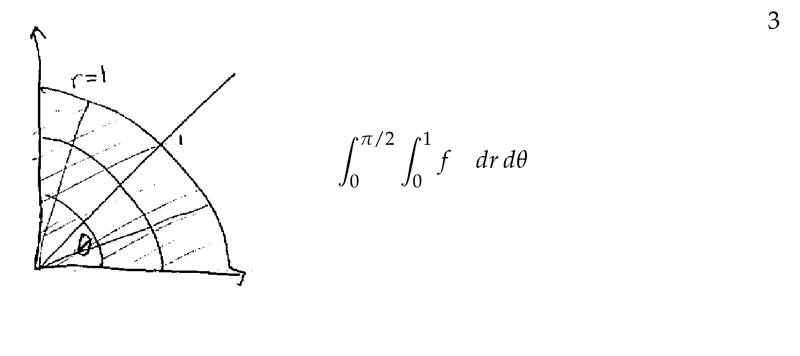
Figure 3: Setting up interated integrals on polar coordinates (1)
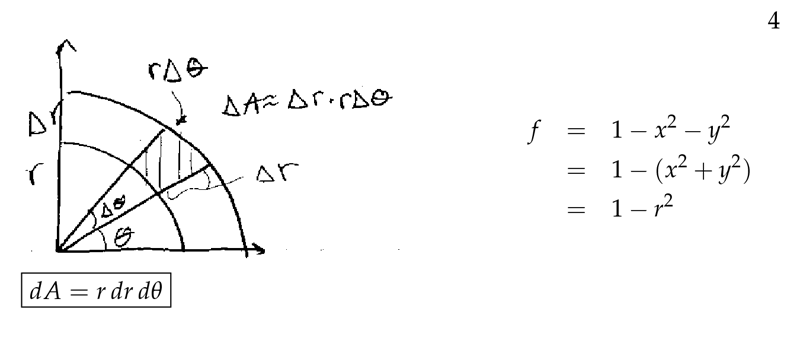
Figure 4: Relationship between \(dA\) and \(d\theta\) and \(dr\)
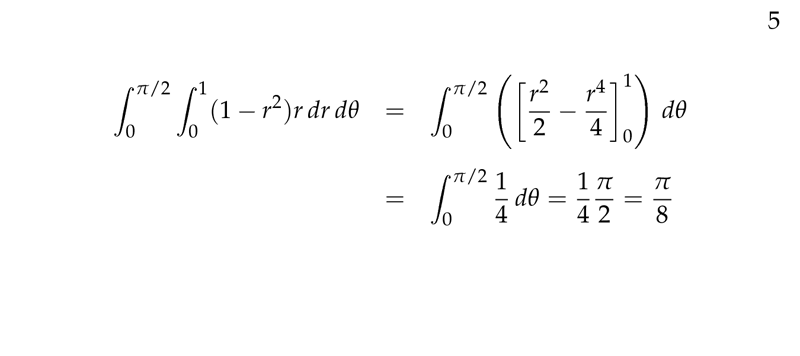
Figure 5: Evaluating the iterated integral
2 How can we set up \(dA\) in polar coordinates (Double integral)?
2.1 Front
How can we set up $dA$ in polar coordinates (Double integral)?
\(\dd{A}\)
Draw a sketch
2.2 Back
\(\dd{A} = r \dd{r} \dd{\theta}\)
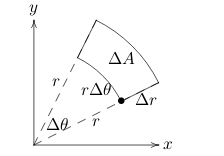
The small curvy rectangle has sides \(\Delta r\) and \(r \Delta \theta\), thus its area satisfies \(\Delta A \approx (\Delta r)(r \Delta \theta)\). As usual, in the limit this become \(\dd{A} = r \dd{r} \dd{\theta}\)
3 How can we set up double integrals in polar coordinates?
3.1 Front
How can we set up double integrals in polar coordinates?
\({\displaystyle \iint_R f(x,y) \dd{A}}\)
3.2 Back
Need to put the equation in polar coordinates, also the limits of the region
- \(x = r \cos \theta\)
- \(y = r \sin \theta\)
- \(\dd{A} = r \dd{r} \dd{\theta}\)
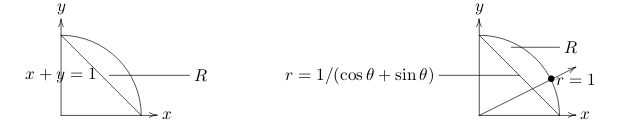
- Hold \(\theta\) fixed, and let \(r\) increase (integrating with respect to \(r\)). It traces out a ray going out from the origin
- Integrate from \(r\text{-value}\) where the ray enters \(R\) to the \(r\text{-value}\) where it leaves (Limits on \(r\))
- Integrate from the lowest value of \(\theta\) for which the corresponding ray intersects \(R\) to the highest value of \(\theta\)
4 Why \(dA = r dr d\theta\) in double integrals in polar coordinates?
4.1 Front
Why $dA = r dr d\theta$ in double integrals in polar coordinates?
Why \(\dd{A} \neq \dd{r} \dd{\theta}\)?
4.2 Back
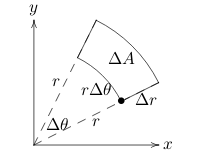
The angle of \(\dd{\theta}\) is at \(r=1\), so the side at any \(r\) is \(r \dd{\theta}\)
5 What represent this equation?
5.1 Front
What represent this equation?
\({\displaystyle x = \sqrt{2y -y^2}}\)
5.2 Back
It’s a circle which center is at point \((0,1)\)
- \(x^2 = 2y - y^2\)
- \(x^2 + y^2 - 2y=0\)
- \(x^2 + (y - 1)^2 - 1 = 0\)
- \(x^2 + (y-1)^2 = 1\)
Polar equation: \(r = 2 \sin \theta\)
6 What is the polar equation of the vertical line \(x = 2\)
6.1 Front
What is the polar equation of the vertical line $x = 2$
\(x = 2\)
6.2 Back
From the origin, we track out a ray with angle \(\theta\). It’s form a right triangle, which hypotenuse is \(r\) and lower side is \(x\).
\(r \cos \theta = 2 \implies r = \frac{2}{\cos \theta} = 2 \sec \theta\)
Similar for horizontal line \(y = y_0\)
7 What is a cardiod?, what is its polar equation?
7.1 Front
What is a cardiod?, what is its polar equation?
7.2 Back
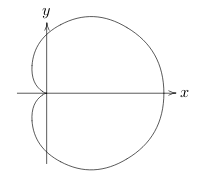
\(r = a(1 + \cos \theta)\)
8 What is a Lemniscate?, what is its polar equation?
8.1 Front
What is a Lemniscate?, what is its polar equation?
8.2 Back
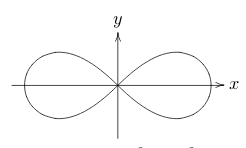
\(r^2 = 2a^2 \cos 2\theta\)
9 What is a Limacon?, what is its polar equation?
9.1 Front
What is a Limacon?, what is its polar equation?
9.2 Back
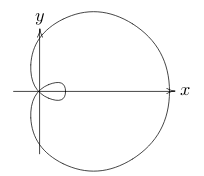
\(r = a(1 + b \cos \theta)\), (\(b>1\))
10 What is a Four leaved rose?, what is its polar equation?
10.1 Front
What is a Four leaved rose?, what is its polar equation?
10.2 Back
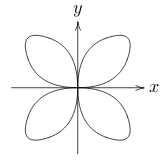
\(r = a \sin 2\theta\)
11 What is the polar equation of a ray?
11.1 Front
What is the polar equation of a ray?
With angle \(\pi/3\)
11.2 Back
\(\theta = \pi/3\)
12 What is the polar equation of a circle at the origin?
12.1 Front
What is the polar equation of a circle at the origin?
Radius: \(3\)
12.2 Back
\(r = 3\)
13 What is the polar equation of a circle at \((a,0)\) touching the origin?
13.1 Front
What is the polar equation of a circle at $(a,0)$ touching the origin?
13.2 Back
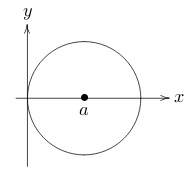
\(r = 2a \cos \theta\), \((-\pi/2 \leq \theta \leq \pi/2)\)