1 Chalkboard

Figure 1: Exchanging order of integration
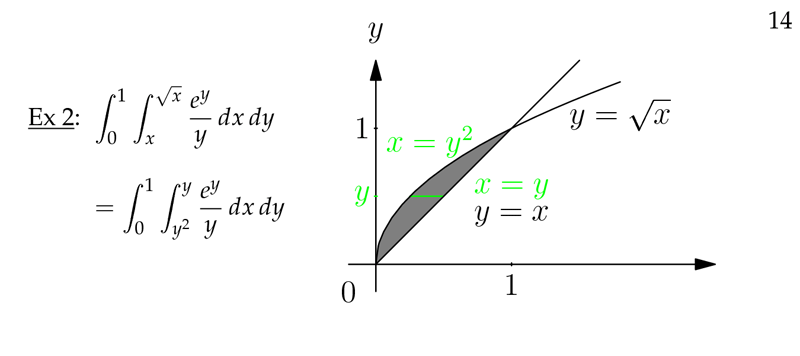
Figure 2: Example of exchanging order of integration
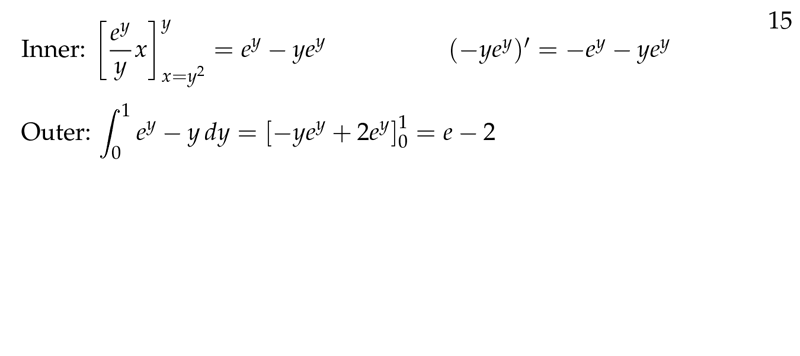
Figure 3: Example conclusion
2 How can we exchanging the order of integration?
2.1 Front
How can we exchanging the order of integration?
Using these example: \({\displaystyle \int_0^2 \int_x^2 e^{-y^2} \dd{y}\dd{x}}\)
2.2 Back
- Draw the graph of the boundaries, and detect the region
- Calculate the inverse functions
- Keep the function \(e^{-y^2}\), but on exchanging order these will be constants
\({\displaystyle \int_0^2 \int_0^y e^{-y^2} \dd{x} \dd{y}}\)
3 Why is it interesting to exchange the order of integration?
3.1 Front
Why is it interesting to exchange the order of integration?
Using these example: \({\displaystyle \int_0^2 \int_x^2 e^{-y^2} \dd{y}\dd{x}}\)
3.2 Back
Because \(e^{-y^2}\) has no simple antiderivative. Sometimes, iterated integrals are more complex in one way than in the other, so you can exchange order of integration