1 Chalkboard

Figure 1: Example of iterated integral
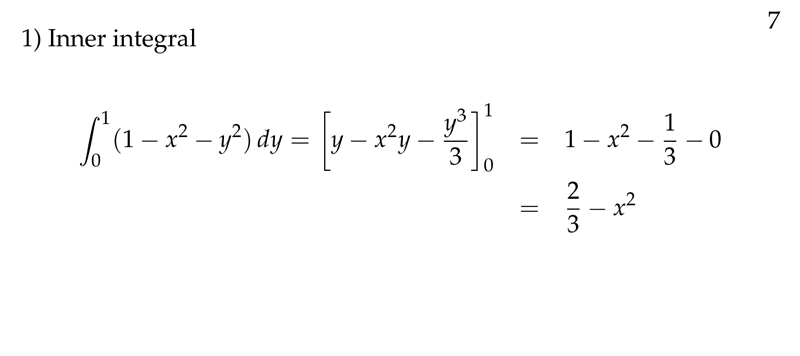
Figure 2: Inner integral
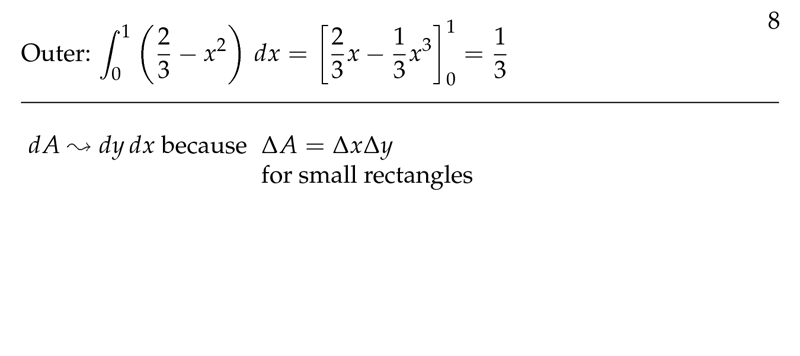
Figure 3: Outer integral

Figure 4: Same function, other region
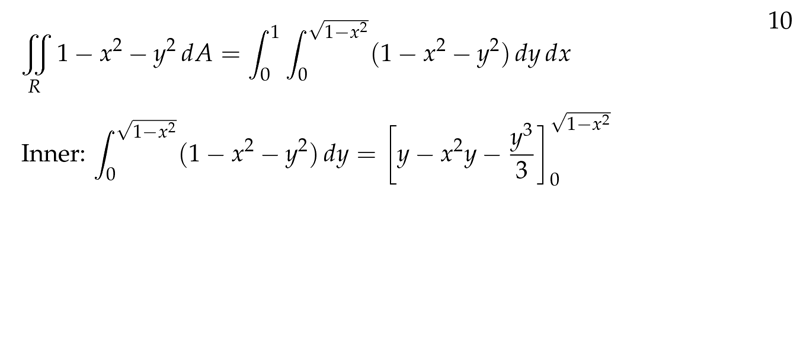
Figure 5: Inner function, more complex region
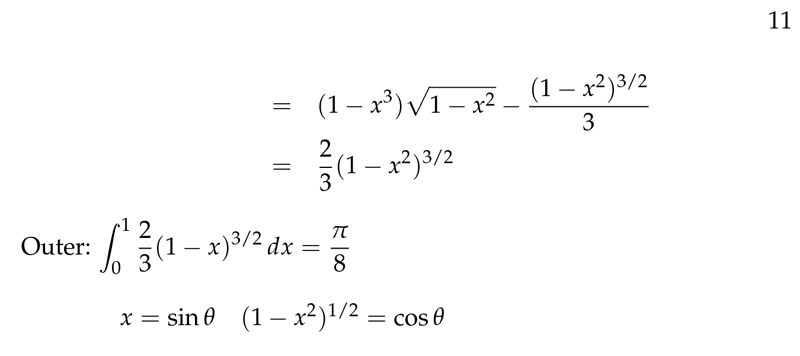
Figure 6: Inner cont., outer function
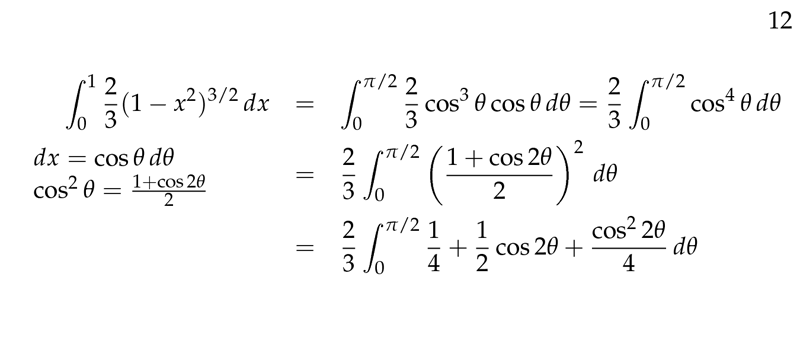
Figure 7: Inner function, trigonometric subtitution
2 How can we write a double integral as a iterated integral?
2.1 Front
How can we write a double integral as a iterated integral?
\(f(x,y)\) over region \(R\)
2.2 Back
\({\displaystyle \iint_R f(x,y) dA}\)
- Region \(R\) is limiting for a range of values of \(x\) and another values of \(y\)
- Outer integral limit, from minimal value of \(x\) to maximum value of \(x\)
- Inner integral limit, depends on a constant value of \(x\), so limit of \(y\) is a function of \(x\)
\({\displaystyle \iint_R f(x,y) dA = \int_{\min{x}}^{\max{x}} \biggl[ \int_{\min{y(x)}}^{\max{y(x)}} f(x,y) dy \biggr] dx}\)
- \(dA = dydx\), because of the area is a very small rectangle, \(\Delta A = \Delta x \Delta y\)
3 Set-up the double integral for this region
3.1 Front
Set-up the double integral for this region
- \(f(x,y)\)
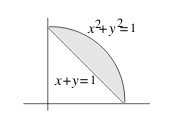
- \(R\) between \(x^2 + y^2=1\) and \(x + y = 1\)
- First integrating with respect to \(y\)
3.2 Back
\({\displaystyle \iint_R f(x,y) \dd{y} \dd{x} = \int_0^1 \int_{1-x}^{\sqrt{1-x^2}} f(x,y) \dd{y} \dd{x}}\)
4 Explain the process to set-up double integral
4.1 Front
Explain the process to set-up double integral
- \(f(x,y)\)
- \(R\) between \(x^2 + y^2 = 1\) and \(x+y=1\)
- First integrating with respect to \(y\)
4.2 Back
- Hold \(x\) fixed, and let \(y\) increase (since we are integrating with
respect to \(y\))
- As the point \((x,y)\) moves, it traces out a vertical line
- Integrate from \(y\text{-value}\) where this vertical line enters the region \(R\) (\(y = 1-x\)), to the \(y\text{-value}\) where it leaves \(R\) (\(y = \sqrt{1-x^2}\))
- Then let \(x\) increase, integrating from the lowest \(x\text{-value}\) (\(0\)) for which the vertical line intersects \(R\), to the highest such \(x\text{-value}\) (\(1\))
\({\displaystyle \iint_R f(x,y) \dd{y} \dd{x} = \int_0^1 \int_{1-x}^{\sqrt{1-x^2}} f(x,y) \dd{y} \dd{x}}\)