1 Chalkboard
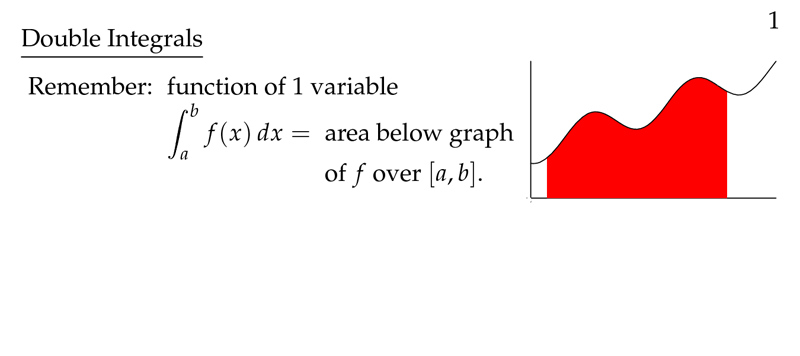
Figure 1: Recall integrals of 1 variable function
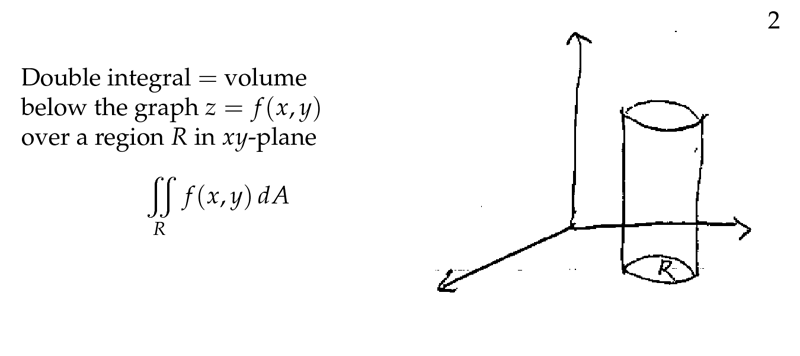
Figure 2: Meaning of double integral
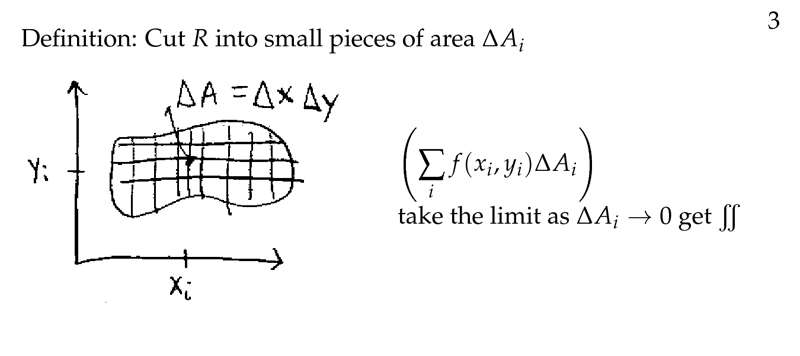
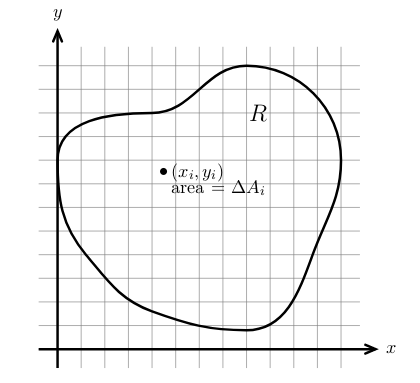
Figure 3: Small pieces of area
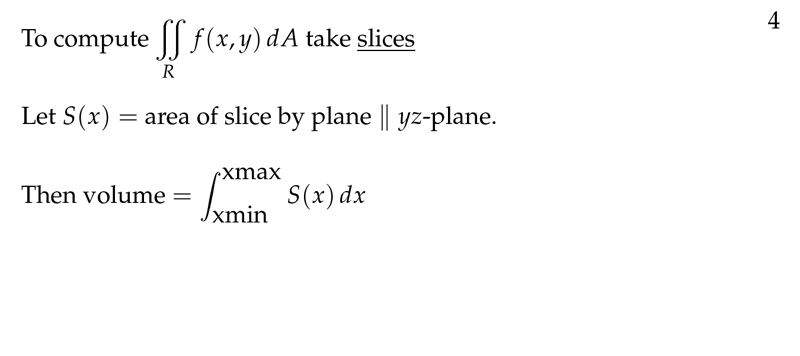
Figure 4: Computing double integrals taking slices
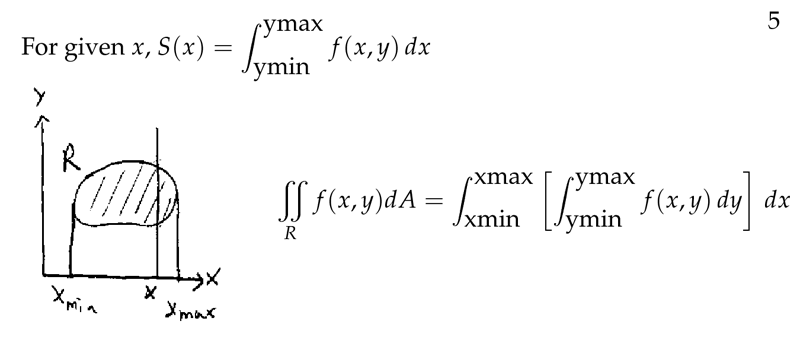
Figure 5: Iterated integrals
2 Can we compute a double integrals as a limit of Riemann sums?
2.1 Front
Can we compute a double integrals as a limit of Riemann sums?
2.2 Back
Yes, you can define a double integral as a sum similarly as 1 variable integrals.
The result of these sum will be the volume under the graph, but these sums can be used to compute areas, volumes, mass, moment of inertia and many other quantities.
3 Which is the definition of double integrals?
3.1 Front
Which is the definition of double integrals?
\(f(x,y)\) and region \(R\)
3.2 Back
\({\displaystyle \iint_R f(x,y) dA = \lim_{\Delta A \to 0} \sum_{i=1}^n f(x_i, y_i) \Delta A_i}\)
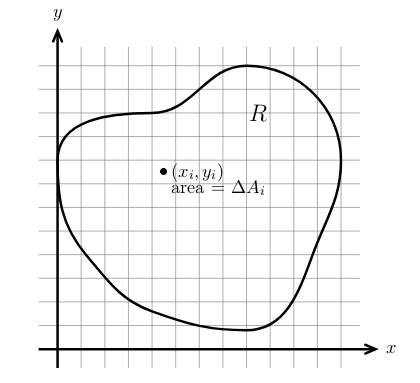
For 18.02: The limit exist and be independent of the specific limiting process. Fractals and other objects don’t satisfy them.
4 Can we use double integrals to compute the area of a region \(R\) in the plane?
4.1 Front
Can we use double integrals to compute the area of a region $R$ in the plane?
4.2 Back
Yes, The area of \(R\) is just the sum of the areas of the pieces
\({\displaystyle \text{area} = \iint_R dA}\)
5 How can set up a double integral to compute the volume?
5.1 Front
How can set up a double integral to compute the volume?
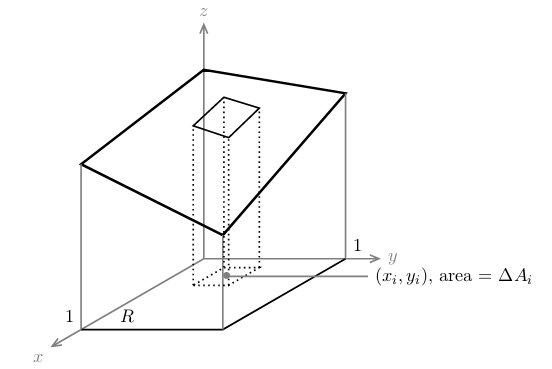
Volume below the graph \(z = f(x,y) = 2 - 0.5(x +y)\) and above the unit square in the \(xy\text{-plane}\)
Explain it with sums
5.2 Back
- Unit square label as \(R\)
- \(R\) is divided into \(n\) small pieces
- For the piece \(i^{\text{th}}\), it contains the point \((x_i,y_i)\)
- Which area is \(\Delta A_i\)
Small Volume: \(\Delta V_i \approx \Delta A_i f(x_i, y_i)\)
Total Volume (as a sum): \({\displaystyle \sum_{i=1}^n \Delta V_i \approx \sum_{i=1}^n \Delta A_i \cross f(x_i, y_i)}\)
As \(n \to \infty\), \(\Delta A_i \to 0\): \({\displaystyle \text{volume} = \iint_R f(x,y) dA}\)