1 Chalkboard
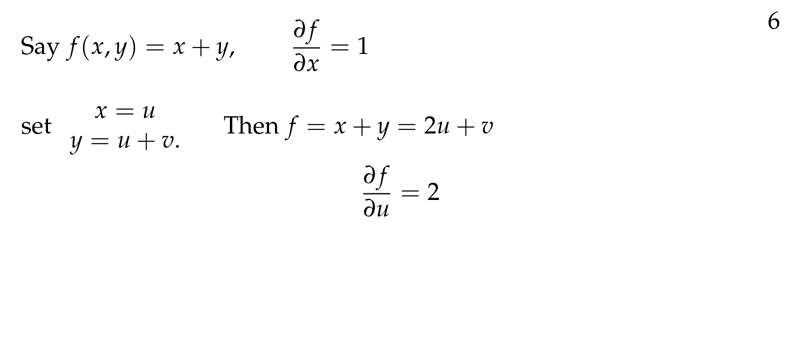
Figure 1: Introduction to confussion
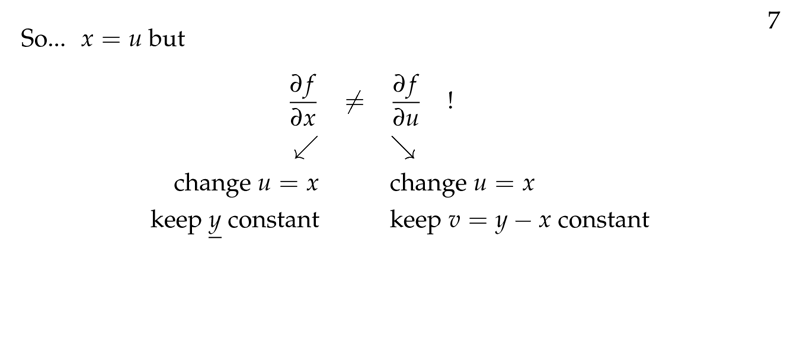
Figure 2: Equals variable but different partial derivatives
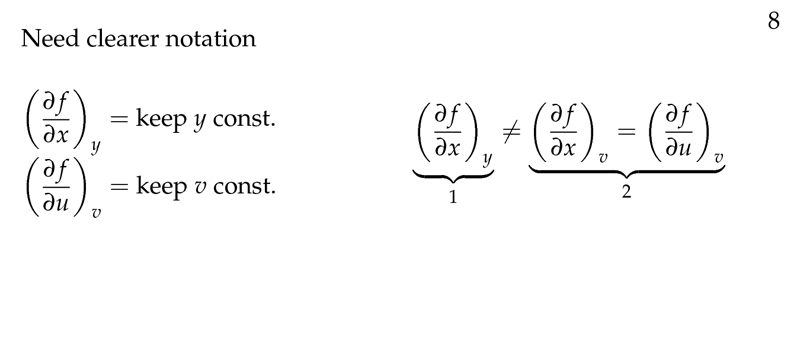
Figure 3: Need clearer notation
2 What differences are there between formal and actual partial derivatives?
2.1 Front
What differences are there between formal and actual partial derivatives?
2.2 Back
- formal partial derivatives, written \(f_x, f_y\), are calculated as if all the variables were independent
- actual partial derivatives, written \(\pdv*{f}{x}\), which take account of any relations between the variables
3 What are the rules for connecting partial derivatives?
3.1 Front
What are the rules for connecting partial derivatives?
- Variables: \(x,y,z\)
- Any two are independent
- Any three are connected by an equation
3.2 Back
- reciprocal rule
- \({\displaystyle \biggl(\pdv{x}{y} \biggr)_z \biggl(\pdv{y}{x} \biggr)_z = 1}\)
- \({\displaystyle \biggl(\pdv{x}{y} \biggr)_z = \frac{1}{(\pdv*{y}{x})_z}}\)
- chain rule
- \({\displaystyle \biggl(\pdv{x}{y} \biggr)_z \biggl(\pdv{y}{t} \biggr)_z = \biggl(\pdv{x}{t} \biggr)_z}\)
- \({\displaystyle \biggl(\pdv{x}{y} \biggr)_z = \frac{(\pdv*{x}{t})_z}{(\pdv*{y}{t})_z}}\)
- cyclic rule
- \({\displaystyle \biggl(\pdv{x}{y} \biggr)_z \biggl(\pdv{y}{z} \biggr)_x \biggl(\pdv{z}{x} \biggr)_y = -1}\)
- \({\displaystyle \biggl(\pdv{x}{y} \biggr)_z = - \frac{(\pdv{x}{z})_y}{(\pdv{y}{z})_x}}\)
4 Get actual partial derivative in terms of formal derivatives of \(w\) and \(r\)
4.1 Front
Get actual partial derivative in terms of formal derivatives of $w$ and $r$
- \(w = w(x,r)\), where \(r = r(x, \theta)\)
- \({\displaystyle \biggl(\pdv{w}{r} \biggr)_{\theta}}\)
4.2 Back
- Independent variables: \(r, \theta\)
- \(x\) depends on them
- \(\theta\) is viewed as a constant
\({\displaystyle \biggl(\pdv{w}{r} \biggr)_{\theta} = w_x \biggl(\pdv{x}{r} \biggr)_{\theta} + w_r}\)
\({\displaystyle \biggl(\pdv{x}{r} \biggr)_{\theta} = \frac{1}{(\pdv*{r}{x})_{\theta}}}\) (reciprocal rule)
\({\displaystyle \biggl(\pdv{w}{r} \biggr)_{\theta} = \frac{w_x}{r_x} + w_r}\)
5 How can you proof reciprocal rule of actual partial derivatives?
5.1 Front
How can you proof reciprocal rule of actual partial derivatives?
Variables \(x,y,z,t\), letting \(z\) fixed
5.2 Back
- As \(z\) is being fixed, each variable became a function of just one other variable
Chain rule: \({\displaystyle \biggl(\pdv{x}{t} \biggr)_z = \biggl(\pdv{x}{y} \biggr)_z \biggl(\pdv{y}{t} \biggr)_z}\)
If \(x = t\), we get an special case of chain rule, called reciprocal rule
\({\displaystyle 1 = \biggl(\pdv{x}{y} \biggr)_z \biggl(\pdv{y}{x} \biggr)_z}\)
6 Which is the chain rule for partial derivative with non-independent variables?
6.1 Front
Which is the chain rule for partial derivative with non-independent variables?
- \(f(x,y,z)\)
- \(g(x,y,z)=c\)
- \({\displaystyle \biggl(\pdv{f}{z} \biggr)_y}\)
6.2 Back
- \({\displaystyle \biggl(\pdv{f}{z} \biggr)_y = \pdv{f}{x} \biggl(\pdv{x}{z} \biggr)_y + \pdv{f}{y} \biggl(\pdv{y}{z} \biggr)_y + \pdv{f}{z} \biggl(\pdv{z}{z} \biggr)_y}\)
- As \(y\) is constant \({\displaystyle \biggl(\pdv{y}{z} \biggr)_y = 0}\)
- And \({\displaystyle \biggl(\pdv{z}{z} \biggr)_y = 1}\)
- Using the constraint (\(g\) is constant):
- \({\displaystyle 0 = \biggl(\pdv{g}{z} \biggr)_y = \pdv{g}{x}
\biggl(\pdv{x}{z} \biggr)_y + \pdv{g}{y} \biggl(\pdv{y}{z}
\biggr)_y + \pdv{g}{z} \biggl(\pdv{z}{z} \biggr)_y}\)
- \({\displaystyle 0 = g_x \biggl(\pdv{x}{z} \biggr)_y + g_z \implies \biggl(\pdv{x}{z} \biggr)_y = - \frac{g_z}{g_x}}\)
Plugin in \({\displaystyle \biggl(\pdv{x}{z} \biggr)_y}\):
\({\displaystyle \biggl(\pdv{f}{z} \biggr)_y = f_x \biggl( - \frac{g_z}{g_x} \biggr) + f_z}\)
7 What does it mean?: constrained partial derivative
7.1 Front
What does it mean?: constrained partial derivative
\({\displaystyle \biggl(\pdv{f}{z} \biggr)_y}\)
- \(f(x,y,z)\), and \(g(x,y,z) = c\)
7.2 Back
- Rate of change of \(f\) with respect to \(z\)
- \(y\) is constant \(\implies \dd{y} = 0\)
- \(z\) varies independently
- \(x\) varies because of \(x(y,z)\), so we need to know how \(x\) varies as \(z\) does: \({\displaystyle \pdv{x}{z}}\). It’s necessary because we need to keep the constraint.