1 Chalkboard

Figure 1: Non-independent variables

Figure 2: \(z\) as a function of \(x\) and \(y\)
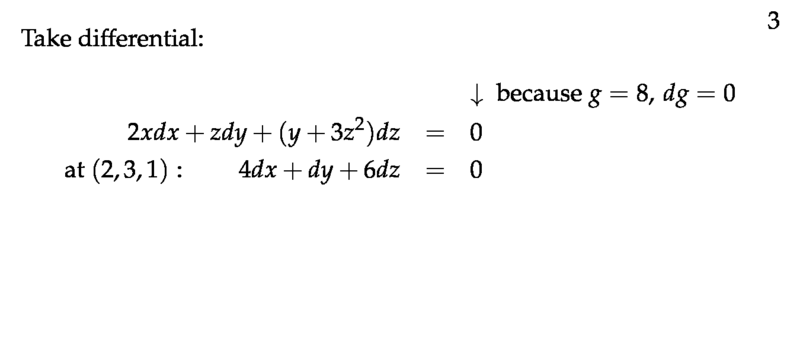
Figure 3: Take differential
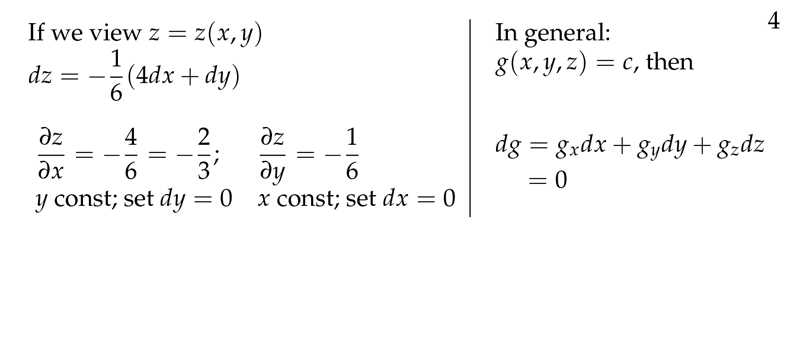
Figure 4: Partial derivatives
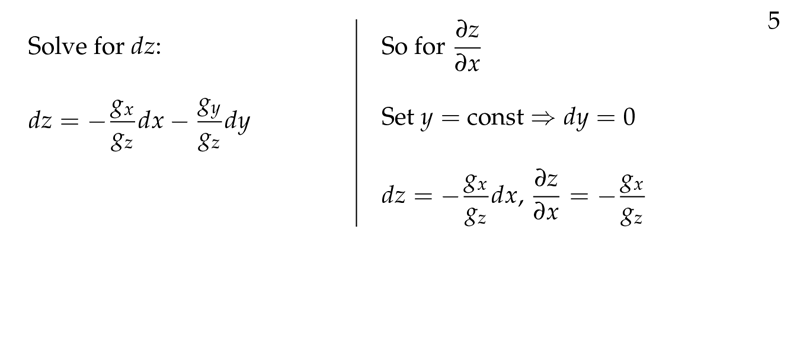
Figure 5: In general
2 What problem can we find when we are computing partial derivatives with non-independent variables?
2.1 Front
What problem can we find when we are computing partial derivatives with non-independent variables?
Example: \(w = x^2 + y^2 + z^2\), \(z = x^2 + y^2\)
\({\displaystyle \pdv{w}{x}}\)
2.2 Back
You need to know which variables are fixed when you are computing partial derivatives. If you have non-independent variable, one of then depends on the others and will be fixed (modifying both variables)
2 cases:
- \(x, y\) are the independent variables: \({\displaystyle \biggl( \pdv{w}{x} \biggr)_y}\)
- \(x,z\) are the independent variables: \({\displaystyle \biggl( \pdv{w}{x} \biggr)_z}\)
3 What differences are there between total differentials and chain rule?
3.1 Front
What differences are there between total differentials and chain rule?
On partial derivatives
3.2 Back
Using chain rule there are less steps, but you only get one partial derivatives. However, using total differentials you get all partial derivatives.
If some variable is non-independent (there is a restricted equation), you need to know its independent partial derivatives.
Using differentials you don’t need to take into account whether the variables are dependent or not. You substitute the differentials you don’t want to.
4 What kind of operation can you do with differentials?
4.1 Front
What kind of operation can you do with differentials?
4.2 Back
- Differentials can be added, subtracted, and multiplied by scalar functions
- One differential can be substituted into another
5 When two differentials are equal?
5.1 Front
When two differentials are equal?
5.2 Back
If variables are independent, and their coefficients are equals
\(A \dd{x} + B \dd{y} + \dots = A_1 \dd{x} + B_1 \dd{y} + \dots \Leftrightarrow A = A_1, B = B_1\)