1 Chalkboard

Figure 1: Directional derivatives
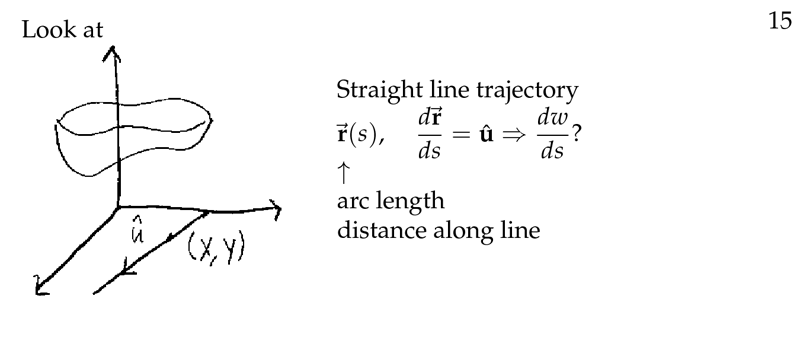
Figure 2: Straight line trayectory

Figure 3: Directional derivative in direction of \(\vu{u}\)

Figure 4: Slope of a slice
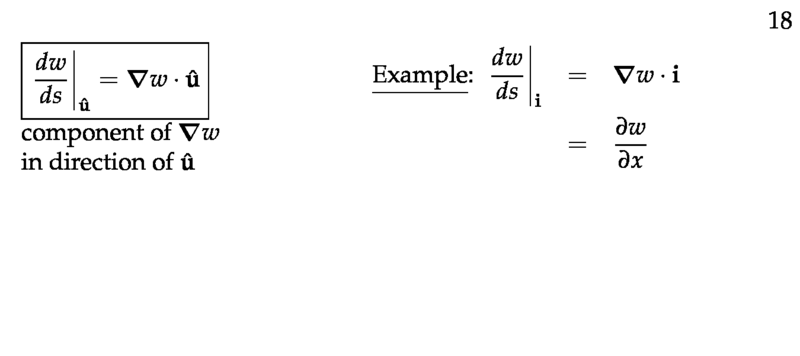
Figure 5: Directional derivative as a components of gradient
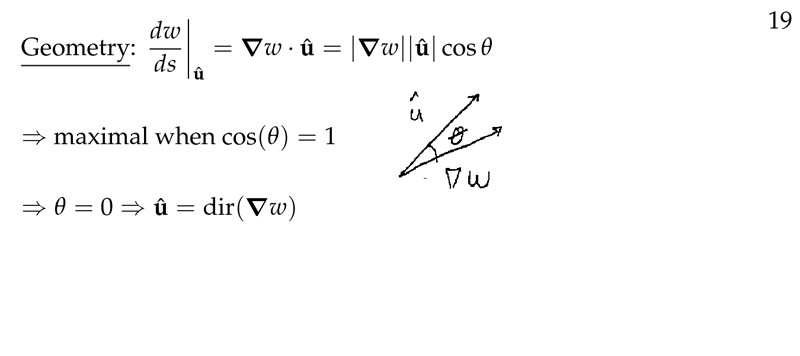
Figure 6: Geometrically
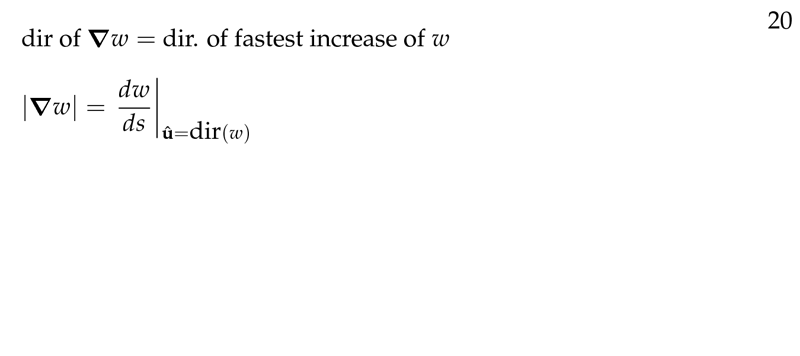
Figure 7: Fastest increase of \(w\)
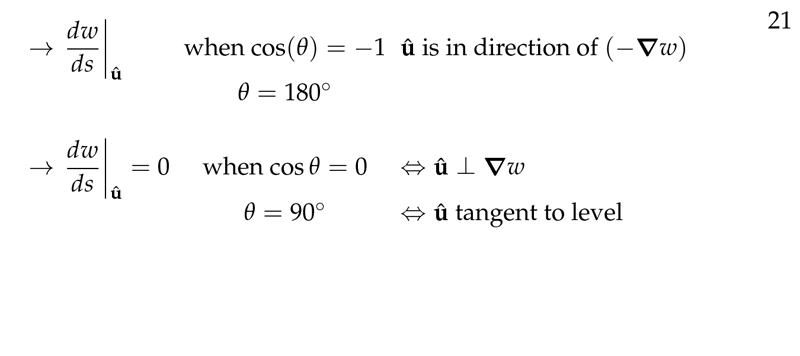
Figure 8: Minimal increase of \(w\) and no increase of w (level curve)
2 What is a directional derivative?
2.1 Front
What is a directional derivative?
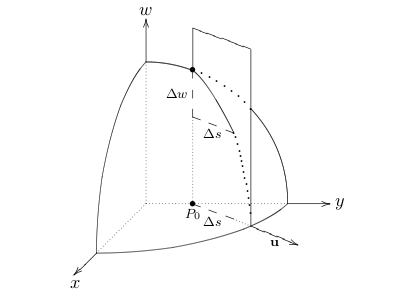
Surface \(w\), direction \(\vu{u}\). Explain how to get it, with \(\Delta\) notation
2.2 Back
It’s the ratio of change of \(w\) with length at the direction of \(\vu{u}\)
The directional derivative of \(w\) at \(P_0\) in the direction \(\vu{u}\) is defined as
\({\displaystyle \dv{w}{s}\bigg|_{P_0,\vu{u}} = \lim_{\Delta s \to 0} \frac{\Delta w}{\Delta s} = \grad{w}(P_0) \vdot \vu{u}}\)
- \(\Delta w\) is the change in \(w\) by a step of length \(\Delta s\) in the direction of \(\vu{u}\)
For example, if \(w = f(x,y)\), \((\Delta s)^2 = (\Delta x)^2 + (\Delta y)^2\)
3 How can you proof that directional derivative is the component of gradient a direction \(\vu{u}\)?
3.1 Front
How can you proof that directional derivative is the component of gradient a direction \(\vu{u}\)?
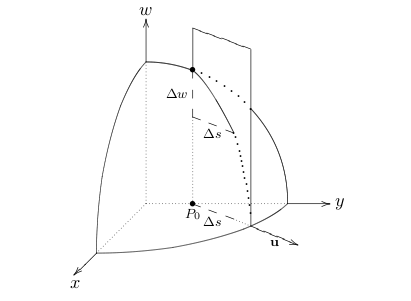
Directional derivative of \(w = f(x,y)\) at point $P0
3.2 Back
How can you proof that directional derivative is the component of gradient a direction \(\vu{u}\)?
- \(\vu{u} = \ev{\frac{\Delta x}{\Delta s}, \frac{\Delta y}{\Delta s}}\), where \((\Delta s)^2 = (\Delta x)^2 + (\Delta y)^2\)
- Tangent plane approximation at \(P_0\)
- \({\displaystyle \Delta w \approx \pdv{w}{x}\bigg|_{P_0} \Delta x + \pdv{w}{y}\bigg|_{P_0} \Delta y}\)
- Dividing by \(\Delta s\)
- \({\displaystyle \frac{\Delta w}{\Delta s} \approx \pdv{w}{x}\bigg|_{P_0} \frac{\Delta x}{\Delta s} + \pdv{w}{y}\bigg|_{P_0} \frac{\Delta y}{\Delta s}}\)
- Write as dot product
- \({\displaystyle \frac{\Delta w}{\Delta s} \approx \ev{\pdv{w}{x}\bigg|_{P_0}, \pdv{w}{y}\bigg|_{P_0}} \vdot \ev{\frac{\Delta x}{\Delta s}, \frac{\Delta y}{\Delta s}}}\)
- \({\displaystyle \frac{\Delta w}{\Delta s} \approx \grad{w}|_{P_0} \vdot \vu{u}}\)
- As \(\Delta s \to 0\)
- \({\displaystyle \dv{w}{s} = \grad{w}|_{P_0} \vdot \vu{u}}\)
As \(\vu{u}\) it’s a unit vector, directional derivative is a component of \(\grad{w}\) at \(\vu{u}\) direction
4 Which is the direction of maximum change of \(w\)
4.1 Front
Which is the direction of maximum change of $w$
\(w = f(x,y)\)
Show up
4.2 Back
Is in the same direction as \(\grad{w}\), where \(\theta\) be the angle between \(\grad{w}\) and direction of change \(\vu{u}\)
\({\displaystyle \dv{w}{s}\bigg|_{\vu{u}} = \grad{w} \vdot \vu{u} = \abs{\grad{w}} \abs{\vu{u}} \cos \theta = \abs{\grad{w}} \cos \theta}\)
It’s obvious that this is greatest when \(\theta = 0\), so \(\grad{w}\) and \(\vu{u}\) are in the same direction