1 Chalkboard
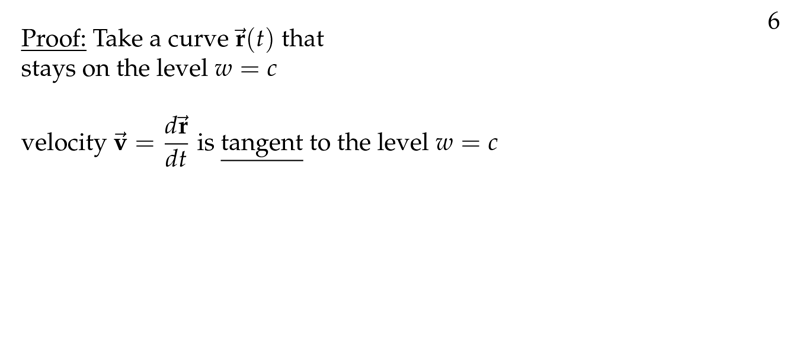
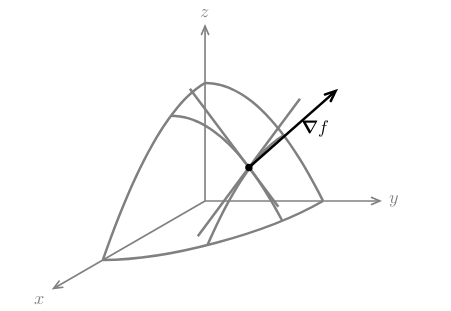
Figure 1: Curve that stays on the level \(w=c\)
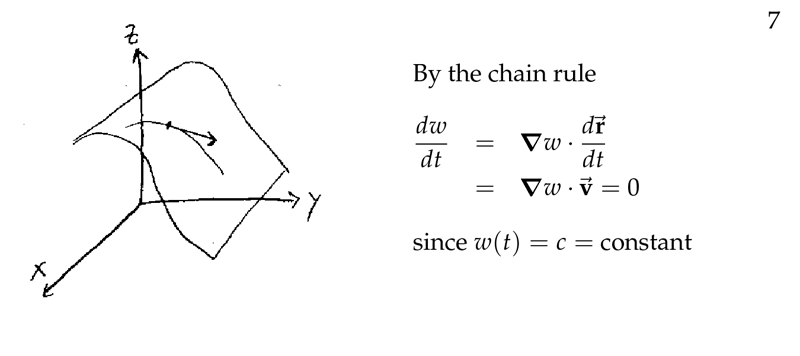
Figure 2: Chain rule
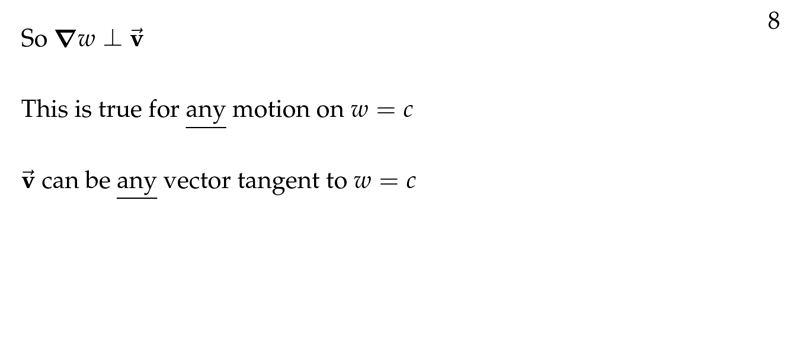
Figure 3: Gradient perpendicular to tangent vector
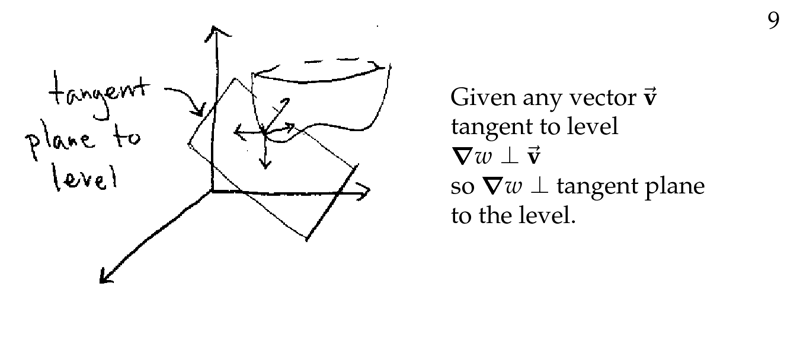
Figure 4: Any vector of tangent plane is perpendicular to gradient
2 How can we proof that gradient is perpendicular to level curves and surfaces?
2.1 Front
How can we proof that gradient is perpendicular to level curves and surfaces?
\(w = f(x,y,z)\), point \(P=(x_0, y_0, z_0)\) and level surface \(f(x,y,z) = c\)
2.2 Back
- Gradient: \(\grad{f}|_P\)
- It means it is perpendicular to the tangent of any curve that lies on the surface and goes through \(P\)
- Let \(\vb{r}(t) = \ev{x(t), y(t), z(t)}\) a curve on the level surface, where \(\vb{r}(t_0)=\ev{x_0, y_0, z_0}\)
- \(w = f(x(t), y(t), z(t))\)
- Level surface: \(g(t) = f(x(t), y(t), z(t)) = c\)
- Differentiating:
- \({\displaystyle \dv{g}{t} = \pdv{f}{x}\bigg|_P \dv{x}{t}\bigg|_{t_0} + \pdv{f}{y} \bigg|_P \dv{y}{t}\bigg|_{t_0} + \pdv{f}{z}\bigg|_P \dv{z}{t}_{t_0} = 0}\)
- \({\displaystyle \dv{g}{t} = \ev{\pdv{f}{x}\bigg|_P, \pdv{f}{y}\bigg|_P, \pdv{f}{z}\bigg|_P} \vdot \ev{\dv{x}{t}\bigg|_{t_0}, \dv{y}{t}\bigg|_{t_0}, \dv{z}{t}\bigg|_{t_0}} = 0}\)
- \({\displaystyle \grad{f}\bigg|_P \vdot \vb{r’}(t_0) = 0}\)
Since, dot product is 0, we have shown that the gradient is perpendicular to the tangent to any curve that lies on the level surface