1 Chalkboard
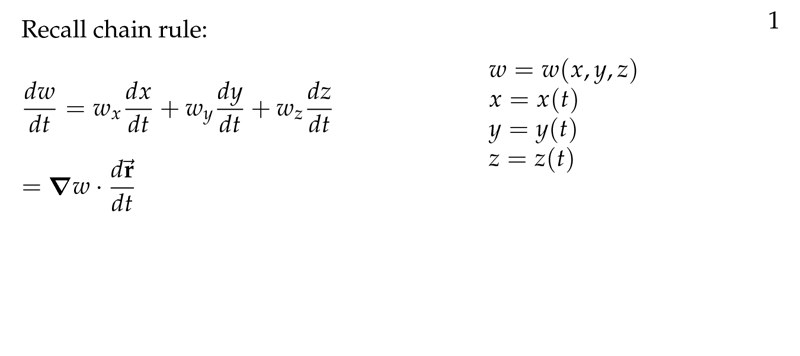
Figure 1: Recall chain rule
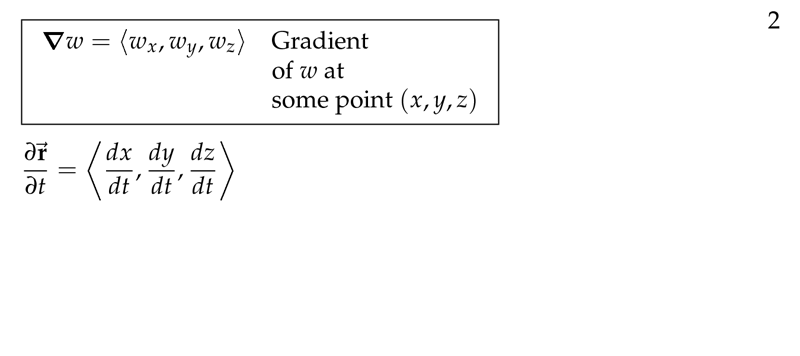
Figure 2: Definition of gradient
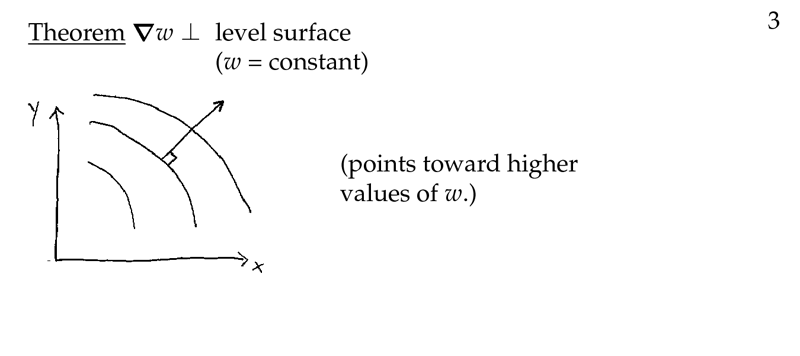
Figure 3: Gradient is perpendicular to level surface

Figure 4: Example of Gradient (1)
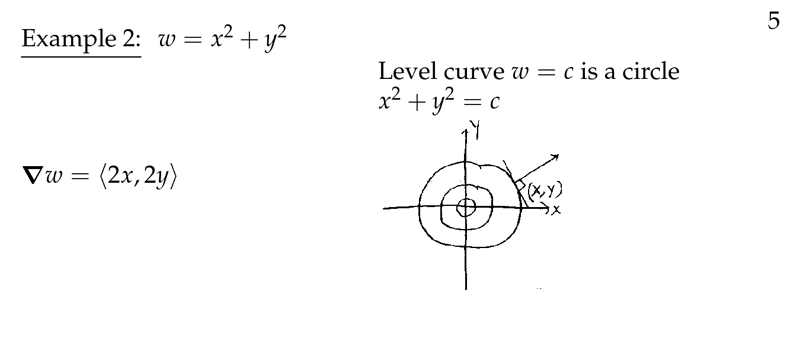
Figure 5: Example of Gradient (2)
2 What is the definition of gradient?
2.1 Front
What is the definition of gradient?
\(w = f(x,y, z)\)
2.2 Back
It’s a vector which components are the rates of changes of \(w\) in the \(\vb{i}\), \(\vb{j}\) and \(\vb{k}\) directions
\({\displaystyle \text{grad } w = \grad w = \ev{\frac{\partial w}{\partial x}, \frac{\partial w}{\partial y}, \frac{\partial w}{\partial z}}}\)
3 Can you evaluate the gradient at some point \((x_{0}, y_{0})\)
3.1 Front
Can you evaluate the gradient at some point $(x_{0}, y_{0})$
\(w = f(x,y)\)
3.2 Back
\({\displaystyle \text{grad } w(x_0, y_0) = \grad w|_{P_0} = \grad w|_0 = \ev{\frac{\partial w}{\partial x} \bigg|_0, \frac{\partial w}{\partial y} \bigg|_0}}\)
4 How is the gradient vector geometrically?
4.1 Front
How is the gradient vector geometrically?
\(w = f(x,y)\)
4.2 Back
It’s a perpendicular vector to the level curves \(f(x,y) = c\)
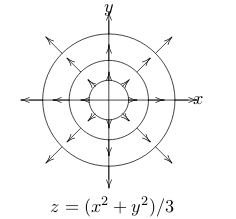
5 What is the radius of the circle \(x^{2} + y^{2} = 5\)?
5.1 Front
What is the radius of the circle $x^{2} + y^{2} = 5$?
5.2 Back
The radius is \(\sqrt{5}\) centered at the origin
6 Which is the direction of gradient vector?
6.1 Front
Which is the direction of gradient vector?
\(w = f(x,y)\)
6.2 Back
It’s point to higher values of \(w\)