1 Chalkboard
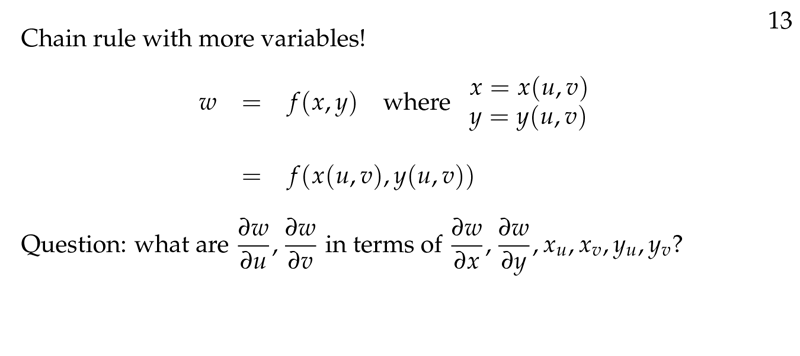
Figure 1: Chain rule with more variables
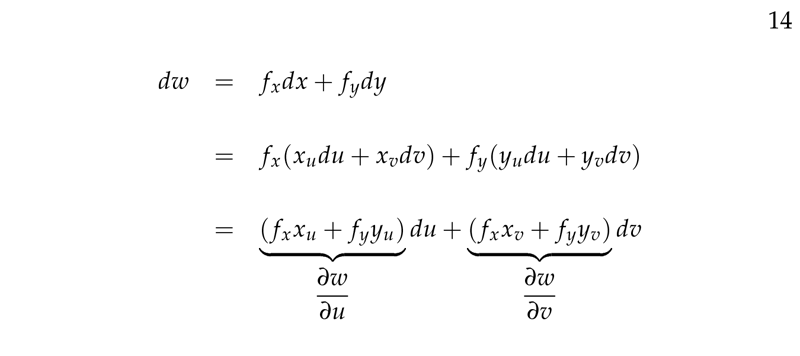
Figure 2: Expansion of chain rule
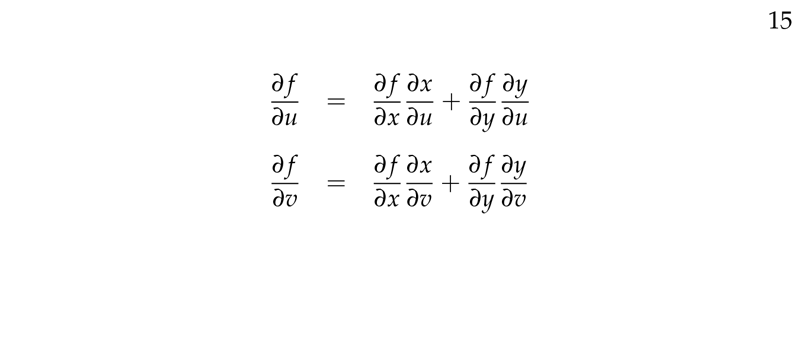
Figure 3: Partial derivative with more variables
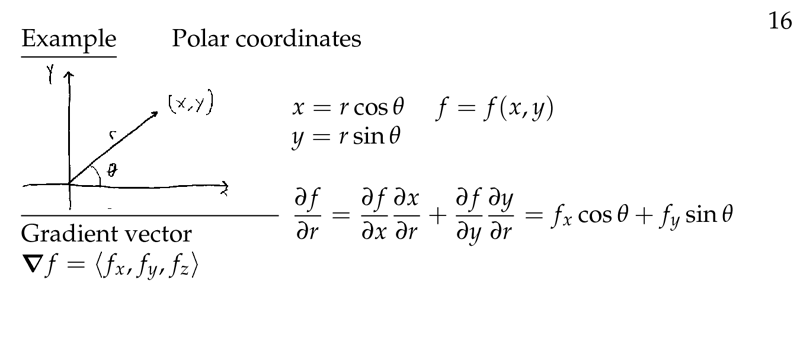
Figure 4: Example with polar coordinates
2 How is the chain rule for partial derivative with more than one independent variable?
2.1 Front
How is the chain rule for partial derivative with more than one independent variable?
\(w=f(x,y)\), and \(x = x(u,v)\), \(y = y(u,v)\)
Get \(\frac{\partial w}{\partial u}\) and \(\frac{\partial w}{\partial y}\)
2.2 Back
For computing \(w\) we need to do a chain of computations
\((u,v) \to (x,y) \to w\)
Where \(w\) is a dependent variable, \(u, v\) are independent variables and \(x,y\) are intermediate variables.
Since \(w\) is a function of \(x\) and \(y\) it has partial derivatives \(\frac{\partial w}{\partial x}\) and \(\frac{\partial w}{\partial y}\)
Ultimately, \(w\) is a function of \(u\) and \(v\)
\({\displaystyle \frac{\partial w}{\partial u} = \frac{\partial w}{\partial x} \frac{\partial x}{\partial u} + \frac{\partial w}{\partial y} \frac{\partial y}{\partial u}}\)
\({\displaystyle \frac{\partial w}{\partial v} = \frac{\partial w}{\partial x} \frac{\partial x}{\partial v} + \frac{\partial w}{\partial y} \frac{\partial y}{\partial v}}\)
3 Get the total differential \(dw\) in terms of \(du\) and \(dv\)
3.1 Front
Get the total differential $dw$ in terms of $du$ and $dv$
\(w=xyz\), \(x = u^2v\), \(y=uv^2\), \(z = u^2 + v^2\)
3.2 Back
\({\displaystyle dw = \frac{\partial w}{\partial x} dx + \frac{\partial w}{\partial y} dy + \frac{\partial w}{\partial z} dz = yz dx + xz dy + xy dz}\)
Double total differential
- \({\displaystyle dx = \frac{\partial x}{\partial u} du + \frac{\partial x}{\partial v} dv = 2uv du + u^2 dv}\)
- \({\displaystyle dy = \frac{\partial y}{\partial u} du + \frac{\partial y}{\partial v} dv = v^2 du + 2uv dv}\)
- \({\displaystyle dz = \frac{\partial z}{\partial u} du + \frac{\partial z}{\partial v} dv = 2u du + 2v dv}\)
Also
\({\displaystyle dw = \frac{\partial w}{\partial u} du + \frac{\partial w}{\partial v} dv}\)
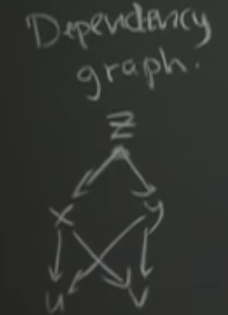
4 How can we build a ‘dependency graph’ for chain rule of multivariable partial derivative?
4.1 Front
How can we build a ‘dependency graph’ for chain rule of multivariable partial derivative?
\(w = w(x,y)\), \(x = x(u,v)\) and \(y = y(u,v)\)
4.2 Back
How can we build a ‘dependency graph’ for chain rule of multivariable partial derivative?