1 Chalkboard
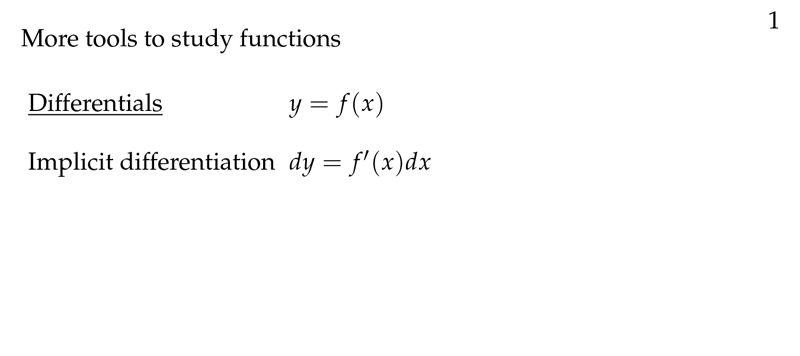
Figure 1: Differentials and implicit differentiation
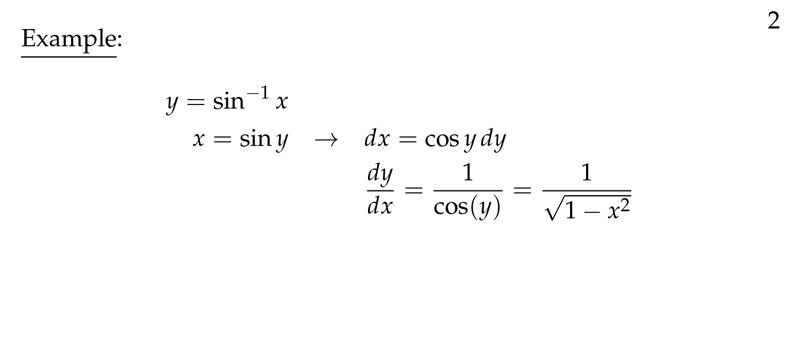
Figure 2: Example of implicit differentiation
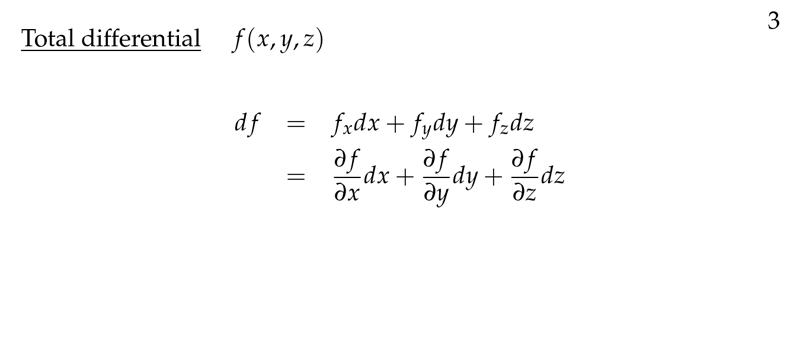
Figure 3: Total differential
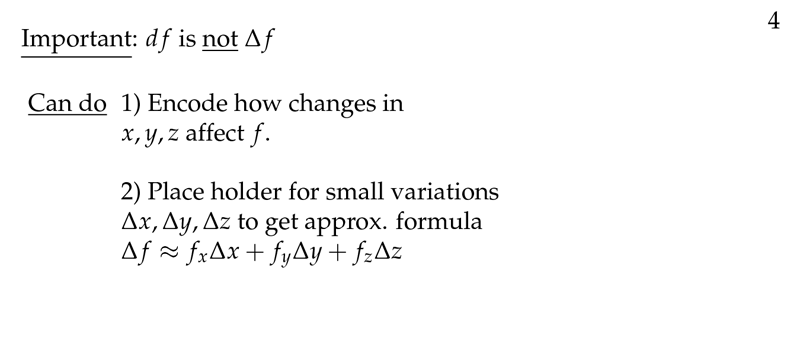
Figure 4: What can do with differentials
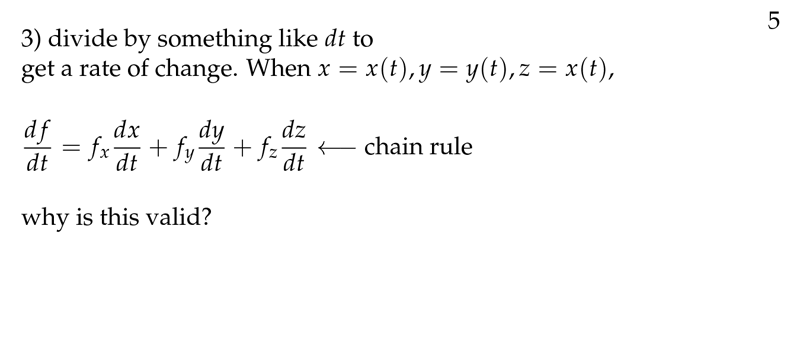
Figure 5: What can do with differentials (2)
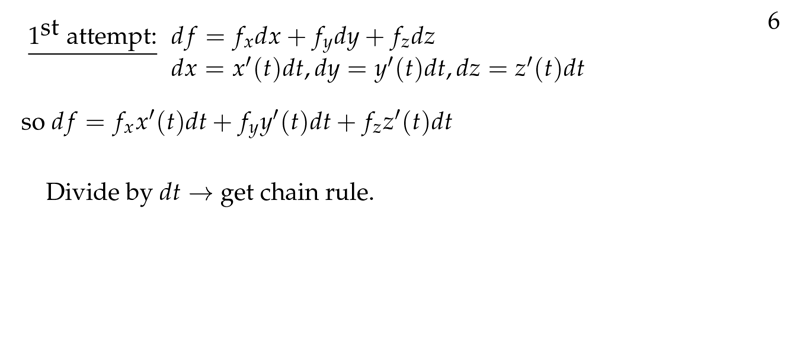
Figure 6: Chain Rule
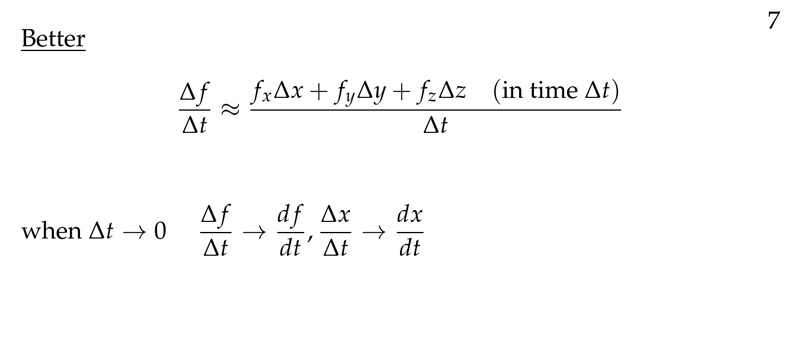
Figure 7: Better approximation in \(\Delta t\)
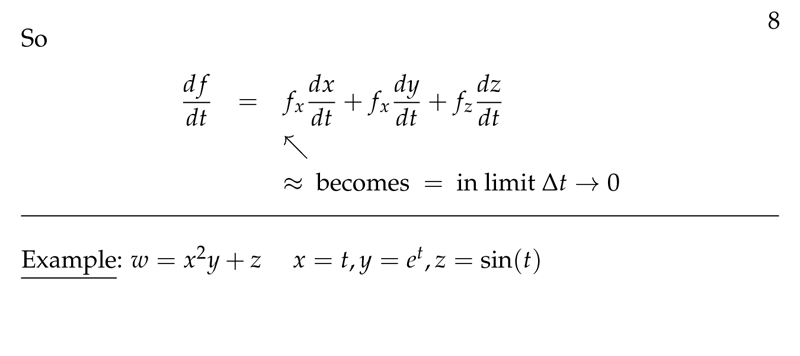
Figure 8: Derivative of multivariable function
2 Is the same \(\Delta f\) that \(df\)
2.1 Front
Is the same $\Delta f$ that $df$
2.2 Back
Not, it isn’t the same. \(\Delta f\) is a number, and \(df\) is a symbol. \(df\) is a number when you write at a ratio of another \(dt\) (\(t\) for example).
3 What is the formula of total differentiation?
3.1 Front
What is the formula of total differentiation?
\(w = f(x,y,z)\)
3.2 Back
\({\displaystyle dw = f_x dx + f_y dy + f_z dz}\)
4 How can we get the total differentiation formula from small variation \(\Delta\)?
4.1 Front
How can we get the total differentiation formula from small variation \(\Delta\)?
\(w = f(x,y,z)\), where \(x = x(t)\), \(y = y(t)\) and \(z = z(t)\)
4.2 Back
How can we get the total differentiation formula from small variation \(\Delta\)?
\(\Delta w \approx f_x \Delta x + f_y \Delta y + f_z \Delta z\)
We can write this approximation as a ratio of \(\Delta t\)
\({\displaystyle \frac{\Delta w}{\Delta t} \approx \frac{f_x \Delta x + f_y \Delta y + f_z \Delta z}{\Delta t}}\)
As \(\Delta t \to 0\), \({\displaystyle \frac{\Delta w}{\Delta t} \to \frac{dw}{dt}}\) (definition of derivative)
\({\displaystyle \frac{dw}{dt} = f_x \frac{dx}{dt} + f_y \frac{dy}{dt} + f_z \frac{dz}{dt}}\)
\({\displaystyle dw = f_x dx + f_y dy + f_z dz}\)
5 How can justify product rule using chain rule of multivariable function?
5.1 Front
How can justify product rule using chain rule of multivariable function?
\(w(u,v) = uv\), where \(u = u(t)\) and \(v = v(t)\)
5.2 Back
\({\displaystyle \frac{dw}{dt} = w_u \frac{du}{dt} + w_v \frac{dv}{dt} = v \frac{du}{dt} + u \frac{dv}{dt} = vu’ + uv’}\)
6 How can justify quotient rule using chain rule of multivariable function?
6.1 Front
How can justify quotient rule using chain rule of multivariable function?
\({\displaystyle w(u,v) = \frac{u}{v}}\), where \(u = u(t)\) and \(v = v(t)\)
6.2 Back
\({\displaystyle \frac{dw}{dt} = w_u \frac{du}{dt} + w_v \frac{dv}{dt} = \frac{1}{v} \frac{du}{dt} - \frac{u}{v^2} \frac{dv}{dt} = \frac{vu’ - uv’}{v^2}}\)