1 Chalkboard
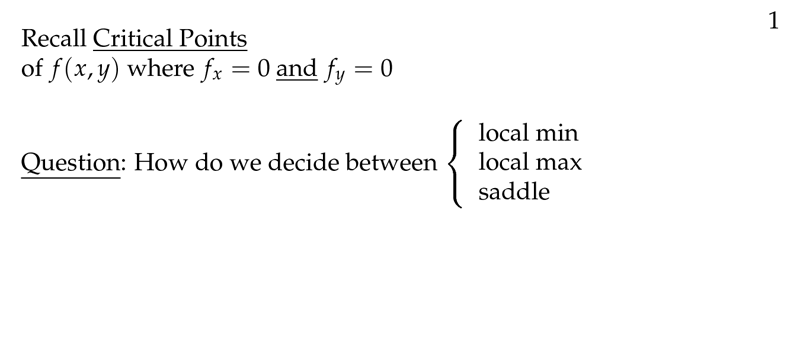
Figure 1: Recall critical points
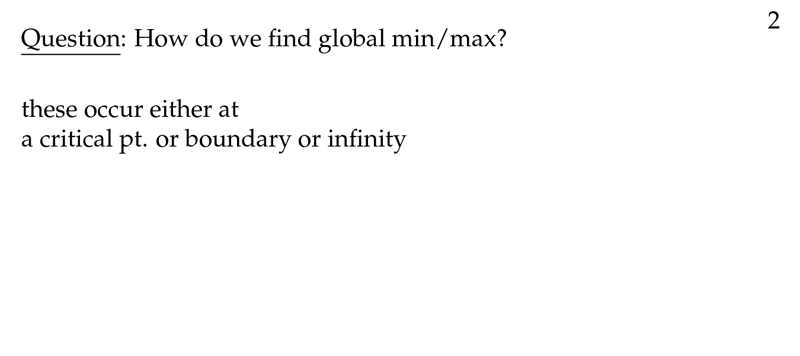
Figure 2: How do we find global min/man?
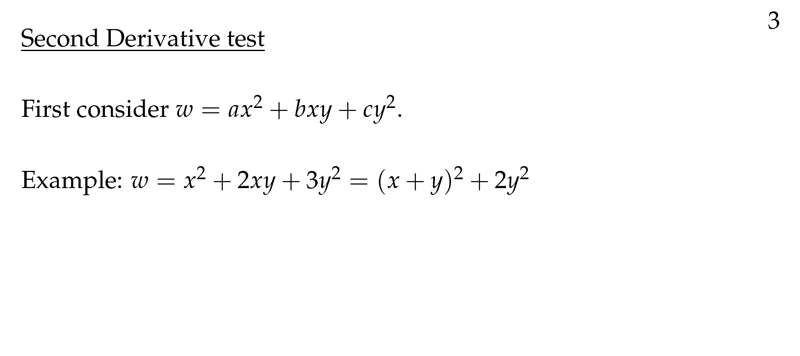
Figure 3: Second derivative test
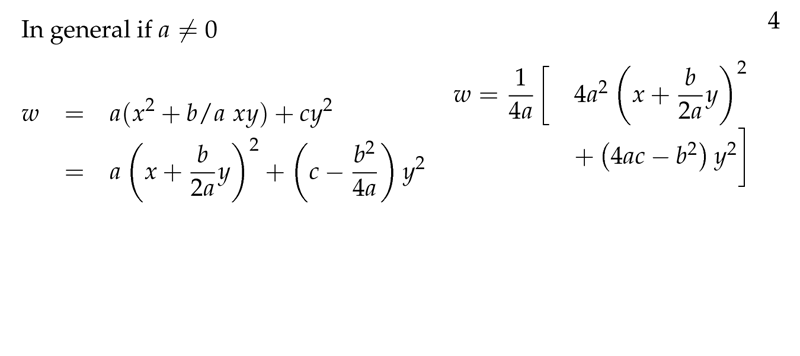
Figure 4: Squared terms
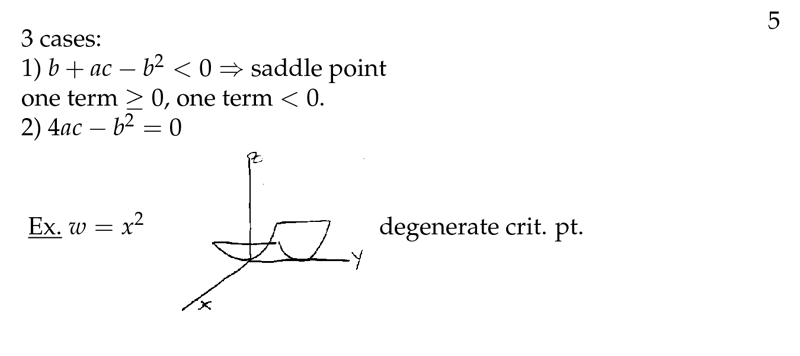
Figure 5: Studying cases
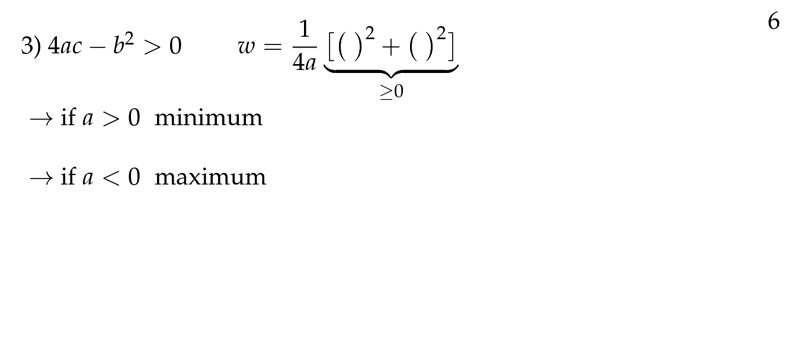
Figure 6: When \(4ac - b^{2} > 0\)
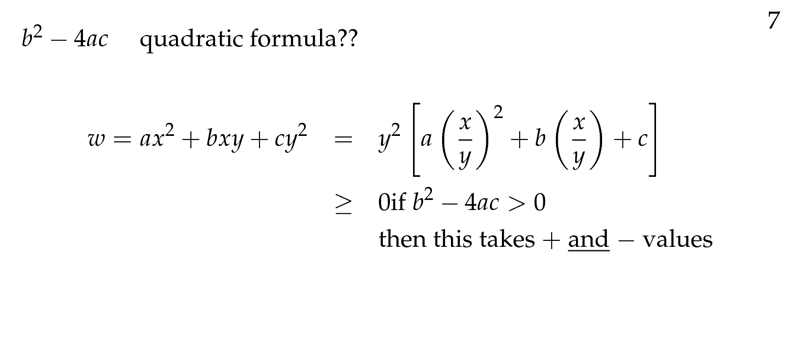
Figure 7: Quadratic formula?
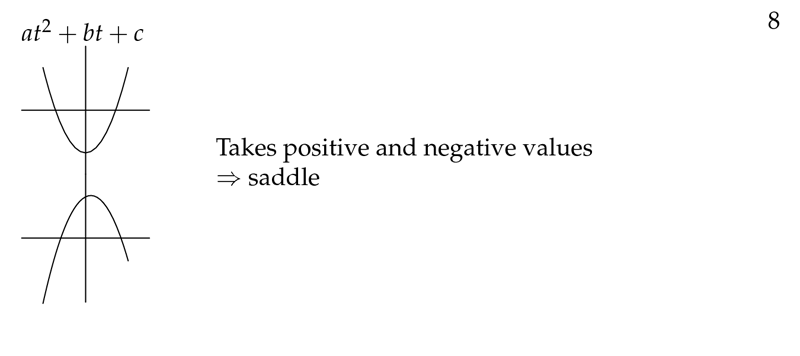
Figure 8: Saddle point
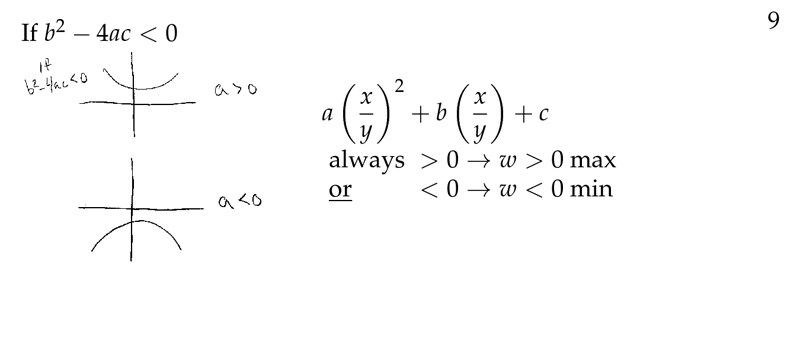
Figure 9: Local max or min
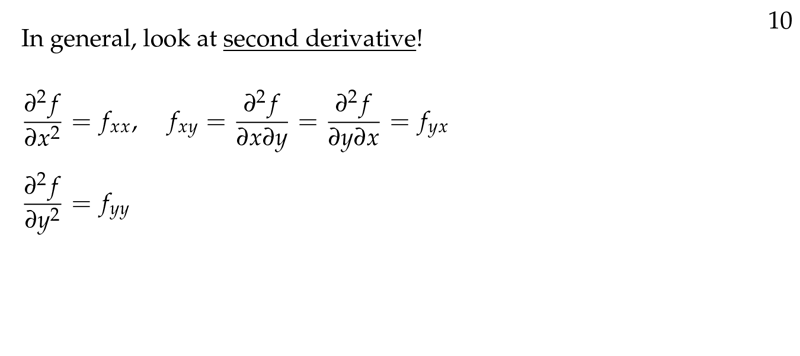
Figure 10: In general, look at second derivative

Figure 11: Second derivative test

Figure 12: Second derivative test cases
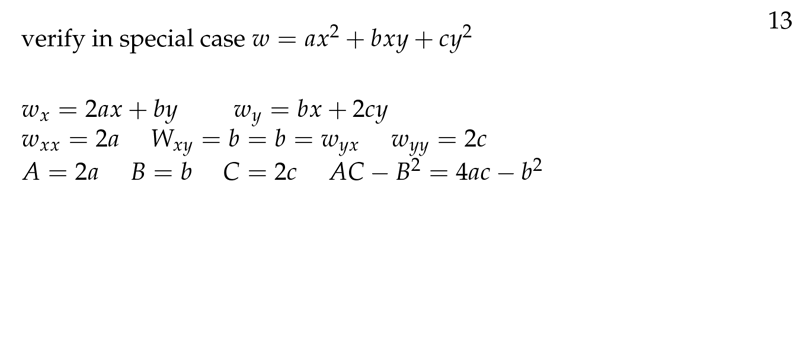
Figure 13: Verify the special case
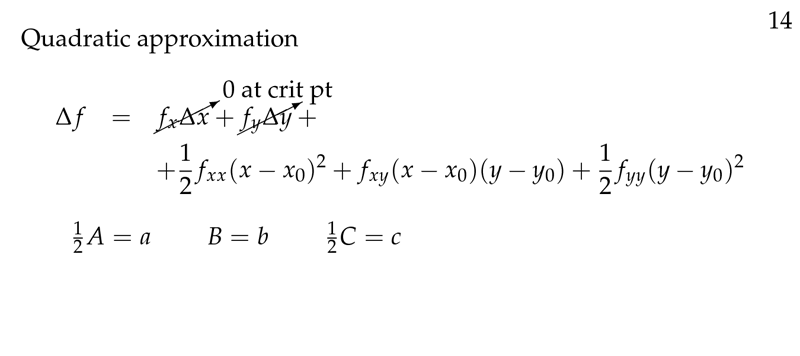
Figure 14: Quadratic approximation of \(f\)

Figure 15: Conclusion of second derivative test
2 Recall second derivative test for 1 variable function
2.1 Front
Recall second derivative test for 1 variable function
2.2 Back
- Find the critical points, where \(f(x) = 0\)
- Apply second derivative for each critical point \(x_0\)
- \(f’’(x_0) > 0 \implies x_0\) is a local minimum point
- \(f’’(x_0) < 0 \implies x_0\) is a local maximum point
- \(f’’(x_0) = 0\), the test fails. You need more information (Could be an inflection point)
The idea behind is
At \(x_0\) the slope of \(f’(x_0)=0\), if \(f’’(x_0)>0\) then \(f’(x)\) is strictly increasing for \(x\) near \(x_0\), so the slope is negative to the left of \(x_0\) and positive to the right. Which shows that \(x_0\) is a minimum point.
The reasoning is similar for local maximum point
3 How many steps do you need to complete for second derivative test
3.1 Front
How many steps do you need to complete for second derivative test for multivariable function?
3.2 Back
- Find the critical points by solving the simultaneous equations
- \(f_x(x,y) = 0\)
- \(f_y(x,y) = 0\)
- The tangent plane at critical point it’s horizontal
- You need 3 second derivatives a these points to determinate max,
min or saddle point. Assuming that these second derivative exists
and are continuous
- \(A = (f_{xx})_0\)
- \(B = (f_{xy})_0 = (f_{yx})_0\)
- \(C = (f_{yy})_0\)
- Compare results with \(AC - B^2\)
4 What are the cases of second derivative test?
4.1 Front
What are the cases of second derivative test?
Let \((x_0,y_0)\) be a critical point of \(f(x,y)\)
- \(A = (f_{xx})_0\)
- \(B = (f_{xy})_0 = (f_{yx})_0\)
- \(C = (f_{yy})_0\)
4.2 Back
- \(AC - B^2 > 0\) and \(A\) and \(C > 0 \implies (x_0,y_0)\) is a minimum point
- \(AC - B^2 > 0\) and \(A\) and \(C < 0 \implies (x_0,y_0)\) is a maximum point
- \(AC - B^2 < 0 \implies (x_0, y_0)\) is a saddle point
If \(AC - B^2 = 0\), the test fails and more investigation is needed
Note: If \(AC - B^2 > 0\), then \(AC > 0\), so that \(A\) and \(C\) must have the same sign.
5 Which is the simplest function to have interesting critical points?
5.1 Front
Which is the simplest function to have interesting critical points?
For second derivative test
5.2 Back
\({\displaystyle w = w_0 + ax + by + \frac{1}{2} (Ax^2 + 2Bxy + Cy^2)}\)
This function has in general a unique critical point
6 Do the second derivative test for this function
6.1 Front
Do the second derivative test for this function
\({\displaystyle w = w_0 + ax + by + \frac{1}{2} (Ax^2 + 2Bxy + Cy^2)}\)
Assume critical point at \((0,0)\)
6.2 Back
- \((w_x)_0 = a\)
- \((w_y)_0 = b\)
- \(w_{xx} = A\)
- \(w_{xy} = B\)
- \(w_{yy} = C\)
7 Which is the Taylor’s approximation of \(f(x,y)\) at a critical point?
7.1 Front
Which is the Taylor’s approximation of $f(x,y)$ at a critical point?
\(f(x,y)\) at critical point \((x_0, y_0)\)
7.2 Back
\({\displaystyle w \approx w_0 + \biggl(\frac{\partial w}{\partial x} \biggr)_0 (x - x_0) + \biggl(\frac{\partial w}{\partial y} \biggr)_0 (y - y_0) + \frac{1}{2} \biggl[ \biggl(\frac{\partial^{2} w}{\partial x^2} \biggr)_0 (x - x_0)^2 + 2 \biggl(\frac{\partial^{2} w}{\partial x \partial y} \biggr)_0 (x - x_0)(y - y_0) + \biggl(\frac{\partial^{2} w}{\partial y^2} \biggr)_0 (y - y_0)^2 \biggr]}\)
Supposing that \({\displaystyle \frac{\partial w}{\partial x \partial y} = \frac{\partial w}{\partial y \partial x}}\)
At critical point, \({\displaystyle \biggl(\frac{\partial w}{\partial x} \biggr) = 0}\), and \({\displaystyle \biggl(\frac{\partial w}{\partial y} \biggr) = 0}\), so you can reduce it to
\({\displaystyle w \approx w_0 + \frac{1}{2} \biggl[ \biggl(\frac{\partial^{2} w}{\partial x^2} \biggr)_0 (x - x_0)^2 + 2 \biggl(\frac{\partial^{2} w}{\partial x \partial y} \biggr)_0 (x - x_0)(y - y_0) + \biggl(\frac{\partial^{2} w}{\partial y^2} \biggr)_0 (y - y_0)^2 \biggr]}\)
8 How we can proof the second-derivative test for a general function
8.1 Front
How we can proof the second-derivative test for a general function
8.2 Back
- Get a Taylor’s formula approximation for \(w =f(x,y)\) at critical points \((x_0, y_0)\), and you will get a quadratic function.
- This quadratic function approximation has a max, min or saddle point there, so will \(f(x,y)\).
- \({\displaystyle w - w_0 \approx \frac{1}{2} (Au^2 + 2Buv + Cv^2)}\), where \(A,B,C\) are the second derivatives at critical point, and \(u= x - x_0\) and \(v = y - y_0\)
- Extract information about this quadratic formula, \(AC - B^2\)
9 What can we say about the function from the quadratic formula?
9.1 Front
What can we say about the function from the quadratic formula?
\({\displaystyle f(x) = Ax^2 + 2Bx + C = 0 \implies x = \frac{-B \pm \sqrt{B^2 - AC}}{A}}\)
9.2 Back
- \(AC - B^2 > 0\), \(A\) and \(C \gt 0 \implies f(x) \gt 0\) for all \(x\), there is a minimum
- \(AC - B^2 > 0\), \(A\) and \(C \lt 0 \implies f(x) \lt 0\) for all \(x\), there is a maximum
- \(AC - B^2 < 0 \implies f(x) \gt 0\) for some \(x\), and \(f(x) \lt 0\) for other \(x\)
10 Where do you need to look at when you seek max and min values?
10.1 Front
Where do you need to look at when you seek max and min values?
10.2 Back
- At critical points
- Boundaries
Then substitute values on function for get max/min
11 How do we can calculate the intersection of 2 surfaces?
11.1 Front
How do we can calculate the intersection of 2 surfaces?
11.2 Back
The point of each surface must give the same result, so we get the intersection
12 How can we calculate a parametric form of a surface?
12.1 Front
How can we calculate a parametric form of a surface?
12.2 Back
- Set \(t\) to one value
- You need to know how are the other variables with respect to \(t\)
13 What is the angle of intersection of 2 surface intersection at a point?
13.1 Front
What is the angle of intersection of 2 surface intersection at a point?
13.2 Back
It’s the angle made of their tangent planes.
Get its normals and get the angle between them.
14 Which is the angle between 2 planes?
14.1 Front
Which is the angle between 2 planes?
14.2 Back
It’s the angle between its normals