1 Chalkboard

Figure 1: Least squares interpolation

Figure 2: Find best “a” and “b”
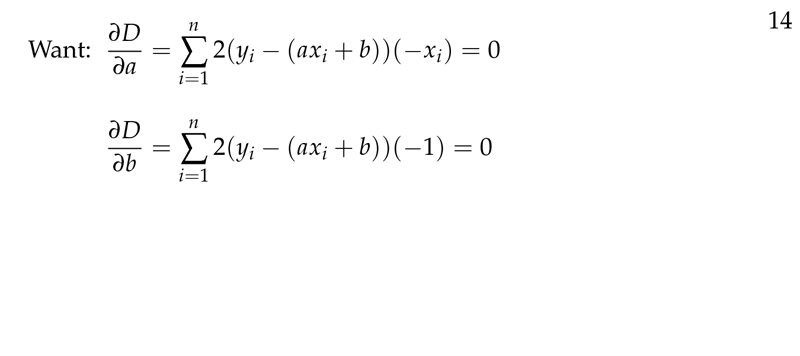
Figure 3: Partial derivatives “a” and “b”
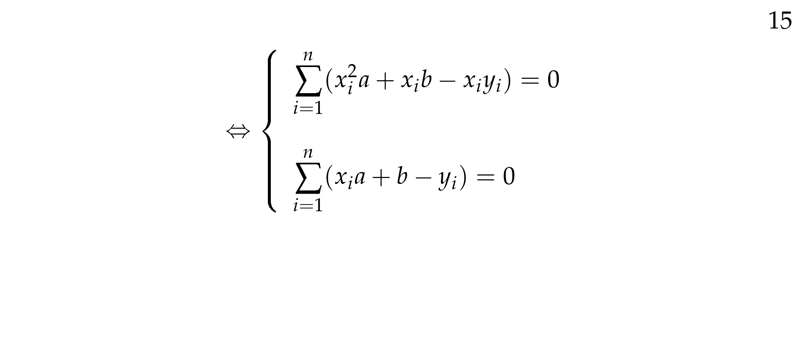
Figure 4: Simply minimization of partial derivatives
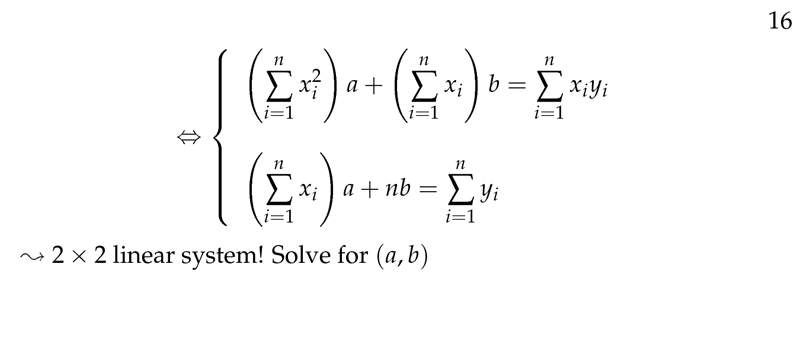
Figure 5: 2x2 Linear system

Figure 6: Least square for exponential data
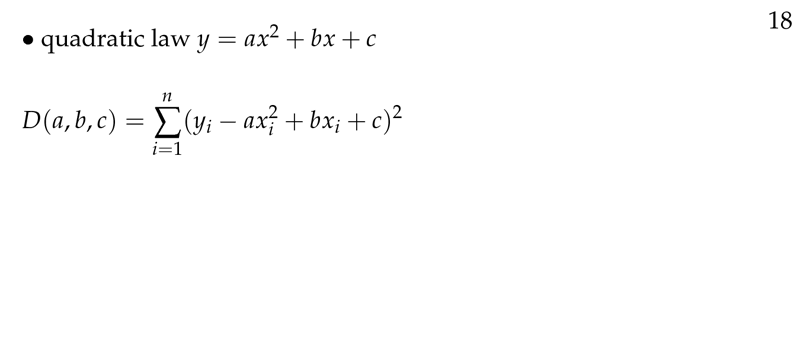
Figure 7: Least squares for quadratic law
2 What is the least-squares curve?
2.1 Front
What is the least-squares curve?
2.2 Back
It’s a simple curve like a line, parabola or exponential which goes approximately through the points, rather than a high-degree polynomial which exactly through them.
3 What is the Lagrange interpolation formula?
3.1 Front
What is the Lagrange interpolation formula?
For \(n\) points
3.2 Back
It’s a curve that pass through all of \(n\) points, using \(n-1\) polynomial degree curve.
It’s really complex formula
4 How can we find a line which goes approximately through a set of data points?
4.1 Front
How can we find a line which goes approximately through a set of data points?
Data points: \((x_1, y_1), (x_2, y_2), \dots, (x_n,y_n)\)
Assume: Errors in measurement are distributed randomly in a Gaussian distribution
4.2 Back
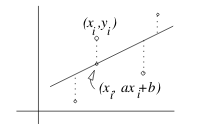
Line: \(y = ac + b\)
Minimizing the sum of deviation: \(D = \sum_{i=1}^n (y_i - (ax_i + b))^2\)
Calculate \(a\) and \(b\) which make \(D\) a minimum, using partial derivatives. Don’t expand the square before differentiate, use chain rule
- \({\displaystyle \frac{\partial D}{\partial a} = \sum_{i=1}^n 2(y_i - ax_i -b)(-x_i) = 0}\)
- \({\displaystyle \frac{\partial D}{\partial b} = \sum_{i=1}^n 2(y_i - ax_i -b)(-1) = 0}\)
Resulting a pair of linear equations
- \({\displaystyle \biggl(\sum x_i^2 \biggr) a + \biggl(\sum x_i \biggr) b = \sum x_i y_i}\)
- \({\displaystyle \biggl(\sum x_i \biggr) a + nb = \sum y_i}\)
5 What is the regression line?
5.1 Front
What is the regression line?
5.2 Back
It’s a line of minimizing the sum of square deviation between estimated line and experimented result.
It’s the line as result of method of least squares. It’s also called leas-squares line.
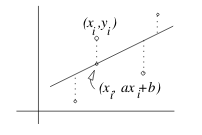
6 What is a deviations for least-squares line?
6.1 Front
What is a deviations for least-squares line?
6.2 Back
It’s the difference between the observed value \(y_i\) and the estimate value from \(y = ax +b\) regression line
7 Why the deviation of least-squares line are squared?
7.1 Front
Why the deviation of least-squares line are squared?
7.2 Back
The reasons are connected with the assumed Gaussian error distribution. So this method ensure that the sum only positive quantities and deviation of opposite sign don’t cancel each other.
It also weights more heavily the larger deviation, keeping experimenters honest, sine they tend to ignore large deviations.
8 What is the sum of the squares of the deviation for a quadratic law?
8.1 Front
What is the sum of the squares of the deviation for a quadratic law?
8.2 Back
\({\displaystyle D = \sum_{i=1}^n (y_i - (a_0 + a_1 x_i + a_2 x_i^2))^2}\)
9 How many variables do you have for a least-square line?
9.1 Front
How many variables do you have for a least-square line?
9.2 Back
2, \(a\) and \(b\)
Estimated line: \(y = ax + b\)
Solving a 2x2 linear system
10 How many variables do you have for a second-degree least-squared curve?
10.1 Front
How many variables do you have for a second-degree least-squared curve?
10.2 Back
3, \(a_0\), \(a_1\) and \(a_2\)
\(y = a_0 + a_1 x + a_2 x^2\)
Solving a 3x3 linear system
11 What is the linear combination of the function \(f_{i}(x)\)
11.1 Front
What is the linear combination of the function $f_{i}(x)$
Where \(f_i(x)\) are given functions
11.2 Back
\(y = a_0 f_0(x) + a_1 f_1(x) + \dots + a_r f_r(x)\)
You can use this linear combination for get a least-square curve. Solving \(a_0, \dots, a_r\) in a square inhomogeneous system of linear equations.
12 How can we use least-squares interpolation for fitting \(ce^{kx}\)?
12.1 Front
How can we use least-squares interpolation for fitting $ce^{kx}$?
12.2 Back
You can fitting using the \(\ln\) of data, and calculate the deviation to the line \(\ln(y) = \ln( c) + kx\)
13 How can you find a least-squared interpolation for \((x, y, z)\)?
13.1 Front
How can you find a least-squared interpolation for $(x, y, z)$?
\(x\) and \(y\) are independent variables and \(z\) is a dependent variable
13.2 Back
\(z = a_1 + a_2 x + a_3y\)
Applying the least-square method, you get a 3x3 linear system for variables \(a_1, a_2, a_3\)
14 Which is the system of equations for least-square line?
14.1 Front
Which is the system of equations for least-square line?
Which solving \(a\) and \(b\), for \(y = ax + b\) and \(n\) points of data
14.2 Back
- \({\displaystyle a \sum_{i=1}^n x_i^2 + b \sum_{i=1}^n x_i = \sum_{i=1}^n x_i y_i}\)
- \({\displaystyle a \sum_{i=1}^n x_i + b n = \sum_{i=1}^n y_i}\)