1 Chalkboard

Figure 1: Applications of Partial Derivatives
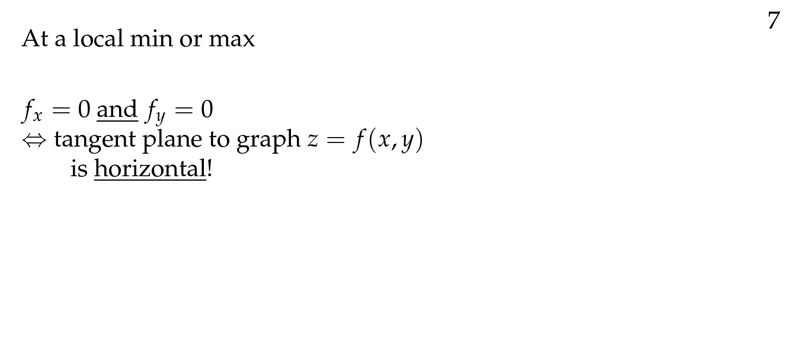
Figure 2: At local min or max
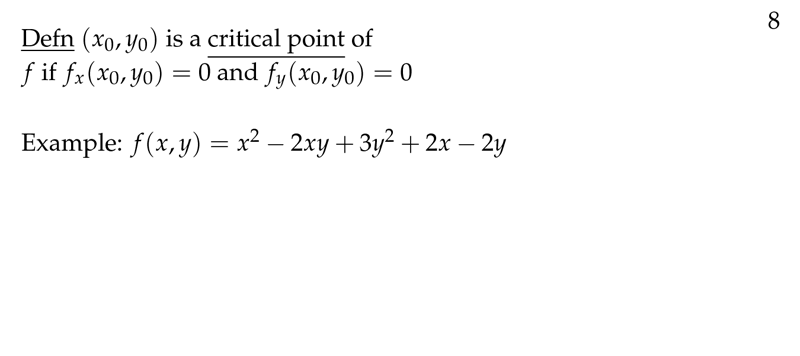
Figure 3: Definition of critical point
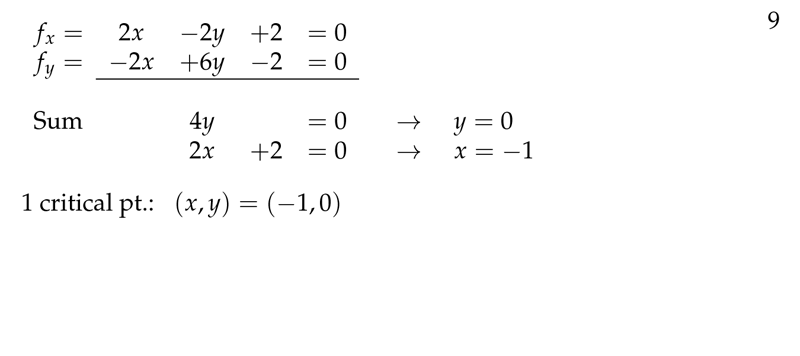
Figure 4: Solve system of equations of partial derivatives
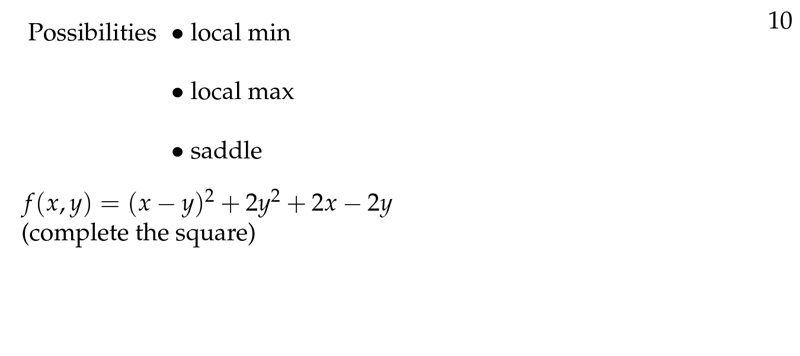
Figure 5: What kind of critical point is it?

Figure 6: Min local point
2 What are the differences between tangent approximation and the equation of the tangent plane?
2.1 Front
What are the differences between tangent approximation and the equation of the tangent plane?
2.2 Back
- In both cases you need a point
- Tangent plane:
- \({\displaystyle z - z_0 = \biggl(\frac{\partial w}{\partial x} \biggr)_0 (x - x_0) + \biggl(\frac{\partial w}{\partial y} \biggr)_0 (y - y_0)}\)
- Tangent approximation formula
- \({\displaystyle \Delta z \approx \biggl(\frac{\partial w}{\partial x} \biggr)_0 \Delta x + \biggl(\frac{\partial w}{\partial y} \biggr)_0 \Delta y}\)
- \({\displaystyle f(x,y) \approx f(x_0, y_0 ) + \biggl(\frac{\partial w}{\partial x} \biggr)_0 (x - x_0) + \biggl(\frac{\partial w}{\partial y} \biggr)_0 (y -y_0)}\)
3 What is a critical point in a multivariable function?
3.1 Front
What is a critical point in a multivariable function?
\(f(x,y)\)
3.2 Back
There is a critical point at \((x_0, y_0)\) when
- \(\biggl(\frac{\partial f}{\partial x} \biggr) (x_0,y_0) = 0\), and
- \(\biggl(\frac{\partial f}{\partial y} \biggr) (x_0,y_0) = 0\), and
Abbreviate: \(f_x = 0\) and \(f_y = 0\)
4 What kind of critical point could found in 2 variable function?
4.1 Front
What kind of critical point could found in 2 variable function?
4.2 Back
- Local max
- Local min
- Saddle (see image)

5 What does happen when tangent plane is horizontal?
5.1 Front
What kind of plane there are in a critical point on 2 variable function?
5.2 Back
Horizontal plane, where \(z\) is constant
\(f_x\) and \(f_y\) at this point is 0 \(\implies\) that the equation of the tangent plane is \(z = z_0\)
6 Are all critical points extrema?
6.1 Front
Are all critical points extrema?
6.2 Back
No, not all critical points are extrema. But the extrema occur at critical point