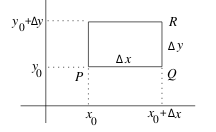
1 Chalkboard
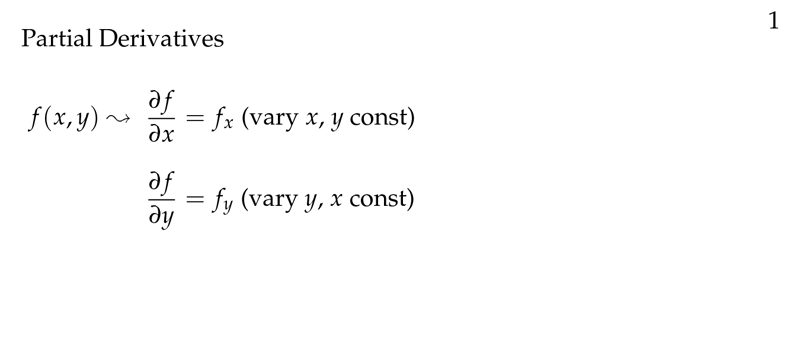
Figure 1: Review partial derivatives

Figure 2: Approximation formula

Figure 3: Justify approximation formula
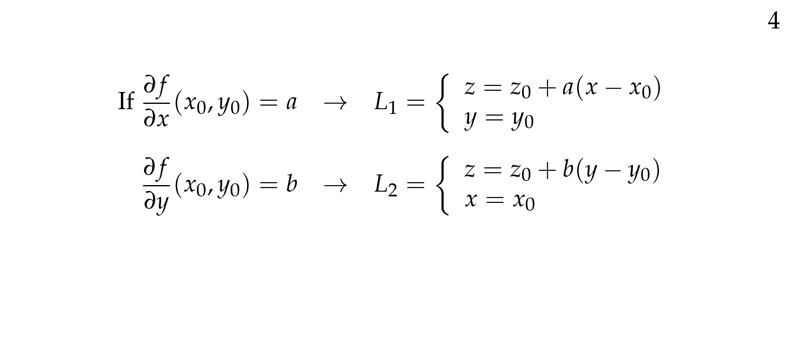
Figure 4: Tangent line to the same point
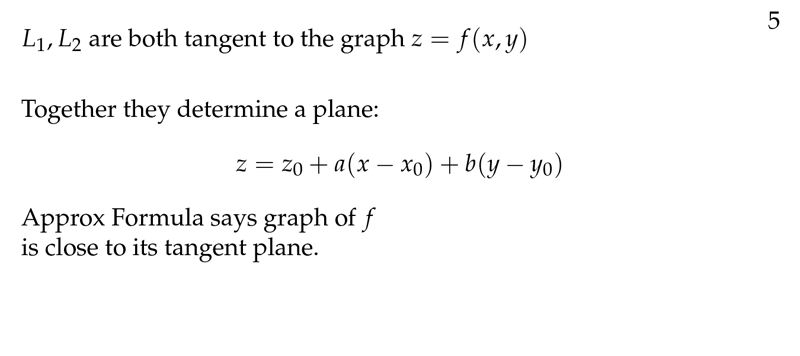
Figure 5: Tagent plane through 2 tangent lines
2 What is a tangent plane?
2.1 Front
What is a tangent plane?
Describe how to get it, and write tangent plane equation
2.2 Back
It’s the plane tangent to a point on a 2 variable functions, that
- Pass through point \((x_0, y_0, w_0)\), where \(w_0 = f(x_0, y_0)\)
- Contain 2 tangent lines of the 2 partial functions
\(A(x - x_0) + B(y - y_0) + C(w - w_0) = 0\)
Assume that plane is not vertical, \(\implies C \neq 0\), so divide through \(C\)
\(w - w_0 = a (x - x_0) + b(y - y_0)\), where \(a = A/C\), \(b=A/C\)
- \(a = \biggl( \frac{\partial w}{\partial x} \biggr)_0\)
- \(b = \biggl( \frac{\partial w}{\partial y} \biggr)_0\)
3 How can we get 2 tangent line on 2 variable functions at a point?
3.1 Front
How can we get 2 tangent line on 2 variable functions at a point?
3.2 Back
- Point \((x_0, y_0, w_0)\), \(w_0 = f(x_0, y_0)\)
- Slope of the tangent line in the \(\vb{i}\) direction (\(y = y_0\))
- \({\displaystyle a = \biggl( \frac{\partial w}{\partial x} \biggr)_0}\)
- Slope of the tangent line in the \(\vb{j}\) direction (\(x = x_0\))
- \({\displaystyle b = \biggl( \frac{\partial w}{\partial y} \biggr)_0}\)
- Line along \(\vb{i}\) direction
- \(z = z_0 + a(x - x_0)\), (\(y = y_0\))
- Line along \(\vb{j}\) direction
- \(z = z_0 + b(y - y_0)\), (\(x = x_0\))
4 Which is the equation of the tangent plane?
4.1 Front
Which is the equation of the tangent plane?
4.2 Back
- \(w_0 = f(x_0, y_0)\)
- \({\displaystyle w = w_0 + \biggl(\frac{\partial w}{\partial x} \biggr)_0 (x - x_0) + \biggl(\frac{\partial w}{\partial y} \biggr)_0 (y - y_0)}\)
You can use gradient too.
5 How can we get an approximation to a 2 variable function?
5.1 Front
How can we get an approximation to a 2 variable function?
5.2 Back
Using the tangent plane on this point
\({\displaystyle f(x, y) \approx w_0 + \biggl(\frac{\partial w}{\partial x} \biggr)_0 (x - x_0) + \biggl(\frac{\partial w}{\partial y} \biggr)_0 (y - y_0)}\)
6 What is the linearization of \(f(x,y)\) at \((x_{0}, y_{0})\)
6.1 Front
What is the linearization of $f(x,y)$ at $(x_{0}, y_{0})$
6.2 Back
Is the approximation whose graph is the the tangent plane at the point \((x_0, y_0, w_0)\), where \(w_0 = f(x_0, y_0)\)
It is the linear function which gives the best approximation to \(f(x,y)\) for values of \((x,y)\) close to \((x_0, y_0)\)
\({\displaystyle f(x,y) \approx w_0 + \biggl(\frac{\partial w}{\partial x} \biggr)_0 (x - x_0) + \biggl(\frac{\partial w}{\partial y} \biggr)_0 (y - y_0)}\)
7 How can we write the linearization of \(f(x,y)\) using \(\Delta\) notation?
7.1 Front
How can we write the linearization of $f(x,y)$ using $\Delta$ notation?
7.2 Back
\(\Delta w \approx \biggl(\frac{\partial w}{\partial x} \biggr)_0 \Delta x + \biggl(\frac{\partial w}{\partial y} \biggr)_0 \Delta y\)
- \(\Delta x = x - x_0\)
- \(\Delta y = y - y_0\)
- \(\Delta w = w - w_0\)
8 Can we write an linear approximation for functions with more than 2 variables?
8.1 Front
Can we write an linear approximation for functions with more than 2 variables?
8.2 Back
Yes, but you can’t use tangent planes and geometry. You use the argument
\(\Delta w \approx \biggl(\frac{\partial w}{\partial x} \biggr)_0 \Delta x + \biggl(\frac{\partial w}{\partial y} \biggr)_0 \Delta y + \biggl(\frac{\partial w}{\partial z} \biggr)_0 \Delta z\)
\(w = f(x,y,z)\)
9 What is the sensitivity principle?
9.1 Front
What is the sensitivity principle?
Tip: Tangent approximation of \(w = f(x,y,\dots)\)
9.2 Back
The numerical value of \(w = f(x,y,\dots)\) calculated at some point \((x_0, y_0, \dots)\), will be most sensitive to small changes in that variable for which the corresponding partial derivative \(w_x, w_y, \dots\) has the largest value at the point
Think about a box, the changes of the volume are more sensitive if we changes the smallest size of the box
10 Why tangent plane could be a good approximation to the surface at \((x_{0}, y_{0}, w_{0})?\)
10.1 Front
Why tangent plane could be a good approximation to the surface at $(x_{0}, y_{0}, w_{0})?$
10.2 Back
It’s the plane with the same slope as the surface in the \(\vb{i}\) and \(\vb{j}\) directions. This means the approximation \({\displaystyle \Delta w \approx \biggl(\frac{\partial w}{\partial x} \biggr)_0 \Delta x + \biggl(\frac{\partial w}{\partial y} \biggr)_0 \Delta y }\) will be good if you move away from \((x_0, y_0)\) in the \(\vb{i}\) direction or \(\vb{j}\) direction.
See Smoothness hypothesis for check if the slope of this plane is the same on any other direction.
11 What is the smoothness hypothesis?
11.1 Front
What is the smoothness hypothesis?
11.2 Back
\(f(x,y)\) is smooth at \((x_0, y_0)\) if \(f_x\) and \(f_y\) are continuous in some rectangle centered at \((x_0,y_0)\)
12 Does the tangent plane have the same slope as the surface in all directions?
12.1 Front
Does the tangent plane have the same slope as the surface in all directions?
12.2 Back
Smoothness hypothesis: \(f(x,y)\) is smooth at \((x_0, y_0)\) if \(f_x\) and \(f_y\) are continuous in some rectangle centered at \((x_0,y_0)\)
It this is true, then the approximation formula of tangent plane it’s true for any direction away from \((x_0, y_0)\)
13 How can we get a proof of linear approximation to multivariable functions?
13.1 Front
How can we get a proof of linear approximation to multivariable functions?
13.2 Back
How can we get a proof of linear approximation to multivariable functions?
This function must be smoothness at the point \((x_0, y_0, \dots)\), so the partial derivatives should be continuous in a neighborhood of this point
You need to calculate the error terms in the approximation