1 Chalkboard
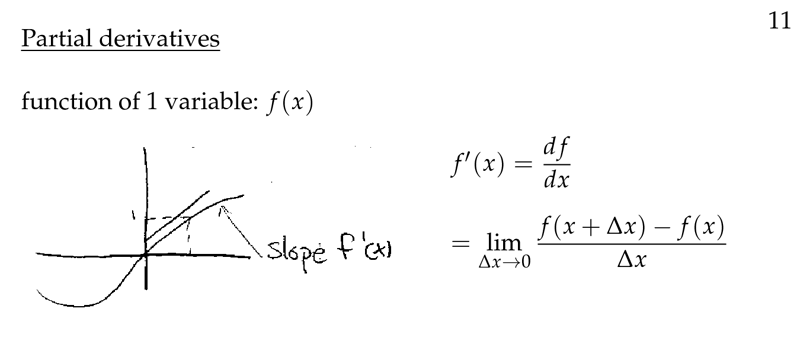
Figure 1: Derivative of a function of 1 variable
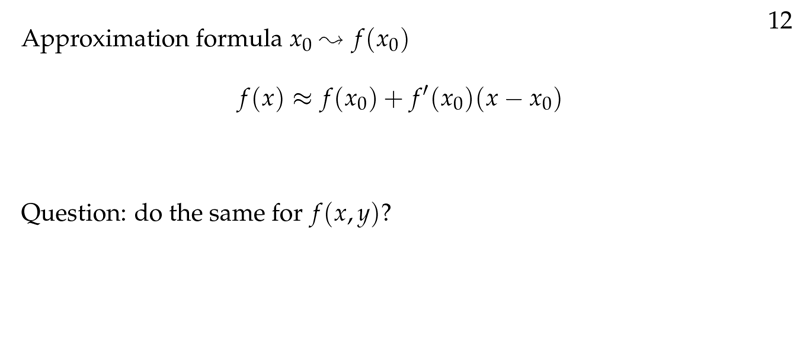
Figure 2: Approximation formula
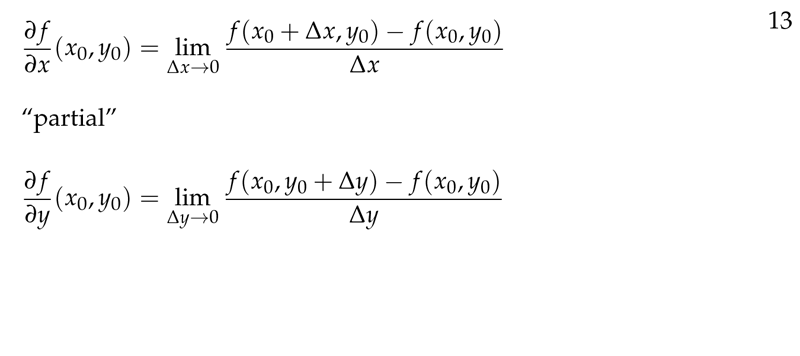
Figure 3: Partial derivative definition
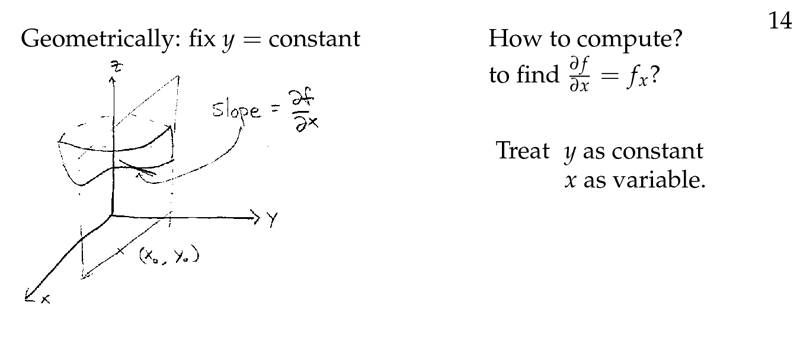
Figure 4: Partial derivative geometrically
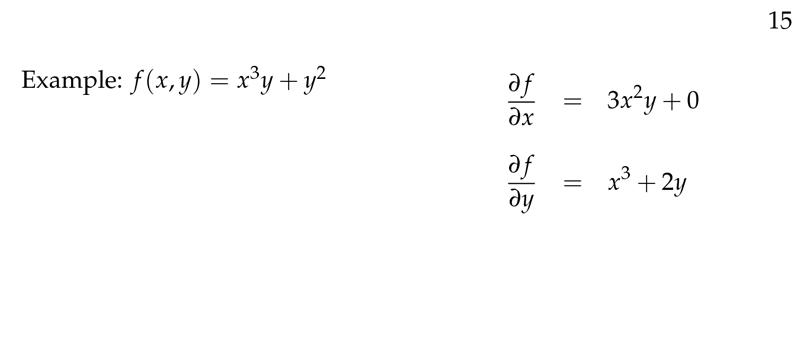
Figure 5: Example of partial derivative
2 What is a partial function of a multivariable function?
2.1 Front
What is a partial function of a multivariable function?
2.2 Back
It’s the function resulting of fixing a value \(y=y_0\) (for example), and just let \(x\) vary (or vice versa).
\(w = f(x, y_0)\), is the partial function for \(y = y_0\)
3 What is a partial derivative?
3.1 Front
What is a partial derivative?
On a function of 2 variables
3.2 Back
It’s a derivative of a 2 variable functions where you see how the function change when one of its variables changes. Gives the rate of changes of \(w\) (partial function) with respect to \(x\) (or another variable)
\({\displaystyle \frac{d}{dx} f(x, y_0) \Big|_{x_0} = \frac{\partial f}{\partial x} \Big|_{(x_0, y_0)}}\)
It’s called partial derivative of \(f\) with respect to \(x\) at the point \((x_0,y_0)\). It tells how fast \(f\) is increasing as \(x\) increases, when \(y\) is held constant.
4 How is it calculated a partial derivative?
4.1 Front
How is it calculated a partial derivative?
4.2 Back
Holding one variable fixed and differentiating with respect to the other variable.
5 How many notations are there for partial derivative?
5.1 Front
How many notations are there for partial derivative?
5.2 Back
Where \(w = f(x,y_0)\) is the partial function for \(y = y_0\)
- \({\displaystyle \frac{\partial f}{\partial x} \bigg|_{(x_0,y_0)}}\)
- \({\displaystyle \frac{d}{dx} f(x, y_0) \bigg|_{x_0}}\)
- \({\displaystyle f_x(x_0, y_0)}\) (Including specific point)
- \({\displaystyle \frac{\partial w}{\partial x} \bigg|_{x_0, y_0}}\) (common in science and engineering)
- \({\displaystyle \biggl(\frac{\partial f}{\partial x} \biggr)_0}\), (indicating the point by just using a single subscript)
- \({\displaystyle \biggl(\frac{\partial w}{\partial x} \biggr)_0}\)
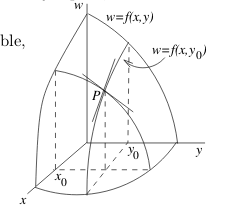
6 What means a partial derivative geometrically?
6.1 Front
What means a partial derivative geometrically?
6.2 Back
7 Can you calculate partial derivative of functions with 3 or more variables?
7.1 Front
Can you calculate partial derivative of functions with 3 or more variables?
7.2 Back
Yes, you can, but you cannot draw geometrically
8 What that does mean on partial derivative?
8.1 Front
What that does mean on partial derivative?
\({\displaystyle \frac{\partial^2 f}{\partial x \partial y}}\)
8.2 Back
First you get partial derivitive \({\displaystyle \frac{\partial f}{\partial y}}\), and then you calculate the partial derivative with respect to \(x\)
\({\displaystyle \frac{\partial}{\partial x} \biggl(\frac{\partial f}{\partial y} \biggr)}\)