1 Chalkboard

Figure 1: Description of kepler’s second law

Figure 2: Kepler’s law in terms of vectors?

Figure 3: Area for second law

Figure 4: Motion of the plane in the same plane

Figure 5: Implications of Kepler’s second law
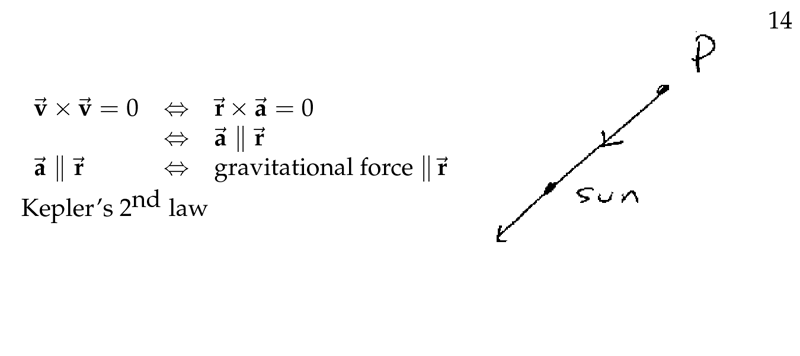
Figure 6: Acceleration vector is parallel to vector position
2 How can we proof that the Kepler’s Second Law is equivalent to the force being central?
2.1 Front
How can we proof that the Kepler’s Second Law is equivalent to the force being central?
Using vectors
2.2 Back
The meaning of ’the radius vector sweeps out area at a constant rate’. Time increasing from \(t\) to \(t + \Delta t\)
\({\displaystyle \Delta A \approx \text{area of the triangle} \approx \frac{1}{2} \abs{\vb{r} \cross \Delta \vb{r}}}\)
\({\displaystyle 2 \frac{\Delta A}{\Delta t} \approx \abs{r \cross \frac{\Delta \vb{r}}{\Delta t}}}\)
As \(\Delta t \to 0\), it’s becomes
\({\displaystyle 2 \frac{dA}{dt} = \abs{\vb{r} \cross \frac{d \vb{r}}{dt}} = \abs{\vb{r} \cross \vb{v}}}\)
If the area is swept out at a constant rate, that means that \(\abs{\vb{r} \cross \vb{v}}\) is constant. Moreover, Kepler’s law says \(\vb{r}\) lies in a plane \(\implies\) \(\vb{v}\) also lies in the same plane.
Hence, we can say \(\vb{r} \cross \vb{v} = \vb{K}\) has constant direction (perpendicular to the plane of motion). \(\vb{K}\) is a constant vector, so \({\displaystyle \frac{d}{dt} (\vb{r} \cross \vb{v}) = \frac{d \vb{r}}{dt} \cross \vb{v} + \vb{r} \cross \frac{d \vb{v}}{dt} = \vb{v} \cross \vb{v} + \vb{r} \cross \vb{a} = \vb{r} \cross \vb{a} = \vb{0}}\)
Which shows that the acceleration vector \(\vb{a}\) is parallel to \(\vb{r}\), but in the opposite direction since the planets do go around the sun. Thus \(\vb{a}\) is directed toward the center, \(\vb{F} = m \vb{a}\) is also directed to the center
Central Force means that force is along vector position
3 How can we get all lines passing through a point and lying in a plane?
3.1 Front
How can we get all lines passing through a point and lying in a plane?
Point \(P_1\) and \(\mathcal{P}\)
3.2 Back
- Check that this point \(P_1\) lying on the plane \(\mathcal{P}\)
- Line with direction \(\ev{a,b,c}\) and same normal as the plane
- All lines through a point: \(\ev{x_0 + at, y_0 bt, z_0 + ct}\)
- Add restriction of \(\ev{a,b,c}\) is perpendicular to the normal with dot product
- You can set the line equation in terms of 2 variable, one of them will be dependent
4 Which is the parametric equation of a point moving around the surface of a sphere?
4.1 Front
Which is the parametric equation of a point moving around the surface of a sphere?
Radius \(a\)
4.2 Back
\(\vb{r}(t) = x(t) \vb{i} + y(t) \vb{j} + z(t) \vb{k}\)
\(x^2(t) + y^2(t) + z^2(t) = a^2\)
5 What we can say if a point is moving around a circle or the surface of a sphere?
5.1 Front
What we can say if a point is moving around a circle or the surface of a sphere?
Let \(\vb{r}(t)\), be the position vector
5.2 Back
We can say that
- \(\abs{\vb{r}}\) is constant to the radius \(a\), so \(\vb{r} \cdot \vb{r} = a^2\)
- Vector velocity \(\vb{v}\) is perpendicular to \(\vb{r}\)
6 Get the derivative of a dot product
6.1 Front
Get the derivative of a dot product
\({\displaystyle \frac{d}{dt} (\vb{r} \cdot \vb{r})}\)
6.2 Back
\({\displaystyle \frac{d}{dt} (\vb{r} \cdot \vb{r}) = \frac{d \vb{r}}{dt} \cdot \vb{r} + \vb{r} \cdot \frac{d \vb{r}}{dt} = 2 \vb{r} \cdot \frac{d \vb{r}}{dt}}\)
7 What we can say if the distance to a moving point is constant?
7.1 Front
What we can say if the distance to a moving point is constant?
7.2 Back
We are moving around a circle or sphere, and velocity is perpendicular to the position vector
8 Can we say that velocity vector is always perpendicular to vector position?
8.1 Front
Can we say that velocity vector is always perpendicular to vector position?
Describe the possible cases
8.2 Back
No, not always only in spheres and circles. The velocity vector is tangent to the vector position
\(\vb{r} \cdot \vb{v} = 0 \implies \frac{d}{dt}\vb{r} \vdot \vb{r} = 0 \implies \vb{r} \cdot \vb{r} = c \implies \abs{r} = \sqrt{c}\), which show that the position is constant. That only happens in circles and spheres.
9 Show that if velocity is perpendicular to the acceleration its speed is constant
9.1 Front
Show that if velocity is perpendicular to the acceleration its speed is constant
\(\vb{v}\) for velocity, \(\vb{a}\) for acceleration
9.2 Back
If \(\vb{v} \cdot \vb{a} = 0\) (perpendicular), then \(\frac{d}{dt}\vb{v} \cdot \vb{v} = 0 \implies \vb{v} \cdot \vb{v} = k \implies \abs{\vb{v}} = \sqrt{k}\).
So the speed is constant
10 What we can say if the speed is constant?
10.1 Front
What we can say if the speed is constant?
\(\abs{v} = k\)
10.2 Back
\(\vb{v} \cdot \vb{v} = k^2 \implies \frac{d}{dt} \vb{v} \cdot \vb{v} = 2 \vb{v} \cdot \vb{a} = 0\).
Hence \(\vb{a}\) and \(\vb{v}\) are perpendicular
11 What does means force is central?
11.1 Front
What does means force is central?
Tip: View Kepler’s second law
11.2 Back
\(\vb{F}\) is central \(\implies \vb{F} = c \vb{r}\), where \(\vb{r}\) is the vector position
Implications (Second Kepler’s law):
- The motion it’s in the plane
- The area is swept out at a constant rate
12 What we can say if…
12.1 Front
What we can say if…
\({\displaystyle \frac{d}{dt} (\vb{r} \cross \vb{v}) = 0}\)
12.2 Back
\(\vb{r} \cross \vb{v} = \vb{K}\), a constant vector
If \(\vb{v}\) is the vector velocity and \(\vb{r}\) is the position vector, then \(\vb{K}\) is perpendicular to \(\vb{r}\), and it’s the normal vector of the plane of motion (because of it’s constant)
13 What is the angle when I roll a wheel at t units to the right?
13.1 Front
What is the angle when I roll a wheel at t units to the right?
- Not slipping
- The center is moving \(t\) units to the right
13.2 Back
- Distance horizontally is equals to the arc length
- \(t = r \cdot \theta\), where \(r\) is the radius
- \(\theta = \frac{t}{r}\)
14 Given a plane equation, get 2 orthogonal vectors in this planes
14.1 Front
Given a plane equation, get 2 orthogonal vectors in this planes
- Result unit vectors
- Plane through origin
14.2 Back
From normal vector of this plane, get a point on the plane and set the unit vector
Get the second vector from cross product of the normal vector and the first result. Get the unit vector