1 Chalkboard

Figure 1: Arc lenght
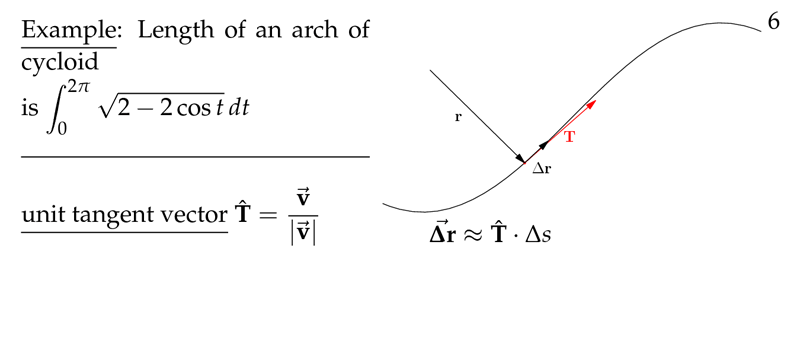
Figure 2: Lenght of an arch of cycloid
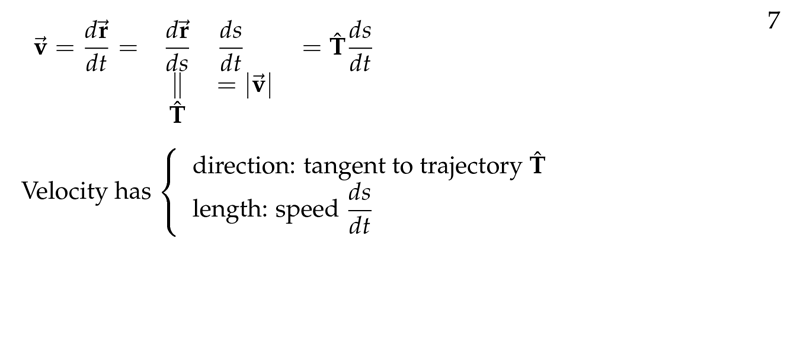
Figure 3: Velocity vector
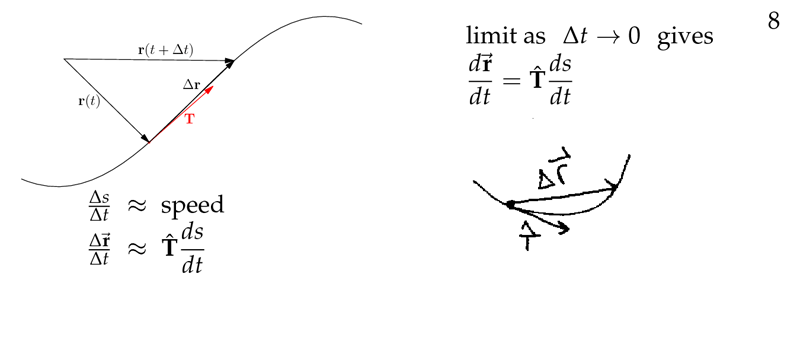
Figure 4: Limit as \(\Delta t \to 0\)
2 What does means speed?
2.1 Front
What does means speed?
Write equation and a diagram
2.2 Back
Speed is the magnitude of the velocity (units of distance per unit time). How hast our moving point is moving (in a parametric curve). Velocity is a vector.
\({\displaystyle \text{speed} = \abs{\vb{v}} = \abs{\frac{d \vb{r}}{dt}} = \frac{ds}{dt}}\)
In the place \({\displaystyle \frac{ds}{dt} = \sqrt{(x’)^2 + (y’)^2}}\)
In space \({\displaystyle \frac{ds}{dt} = \sqrt{(x’)^2 + (y’)^2 + (z’)^2}}\)
Where \(s\) is the distance travelled, or arc length
3 Velocity vs speed
3.1 Front
Velocity vs speed
A point goes one time around a circle of radius 1 unit in 3 seconds. What is its average velocity and average speed?
3.2 Back
Distance travelled equals the circumference of circle \(2 \pi\)
Net displacement is \(\vb{0}\), we return to the same point. \(\Delta \vb{r} = 0\) in one time around
Average speed = distance/time = \(2 \pi /3\)
Average velocity = displacement/time = \(\vb{0}\)
4 What is the distance travelled along a curve?
4.1 Front
What is the distance travelled along a curve?
4.2 Back
Is the length of the curve. We also refer to \(s\) as arc length
5 How can we get the unit tangent vector?
5.1 Front
How can we get the unit tangent vector?
5.2 Back
Is a unit vector in the same direction as the tangent vector \(\vb{T} = \hat{T}\)
\({\displaystyle \vb{T} = \frac{\vb{v}}{\abs{\vb{v}}} = \frac{d \vb{r} / dt}{ds/dt} = \frac{\vb{v}}{ds/dt}}\)
6 Write velocity in terms of unit tangent vector and speed
6.1 Front
Write velocity in terms of unit tangent vector and speed
6.2 Back
\({\displaystyle \vb{v} = \vb{T} \frac{ds}{dt} = \frac{\vb{v}}{ds/dt} \frac{ds}{dt}}\)
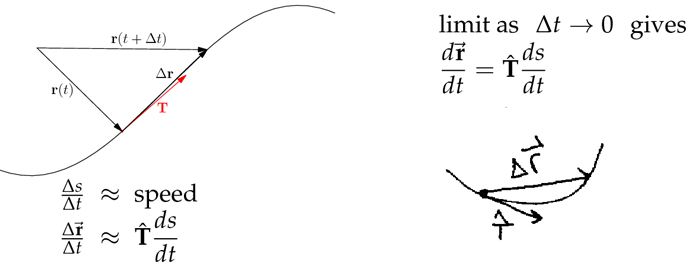
7 Result of \(\Delta\) dot product
7.1 Front
Result of $\Delta$ dot product
\(\vb{r}\) increases by \(\Delta r\), and \(\vb{s}\) increases by \(\Delta s\). What is \(\Delta (\vb{r} \cdot \vb{s})\)
7.2 Back
\({\displaystyle \Delta(\vb{r} \cdot \vb{s}) = (\vb{r} + \Delta \vb{r}) \cdot (\vb{s} + \Delta \vb{s}) - \vb{r} \cdot \vb{s} = \Delta \vb{r} \cdot \vb{s} + \vb{r} \cdot \Delta \vb{s} + \Delta \vb{r} \cdot \Delta \vb{s}}\)