1 Chalkboard

Figure 1: Review parametric equations and position vector
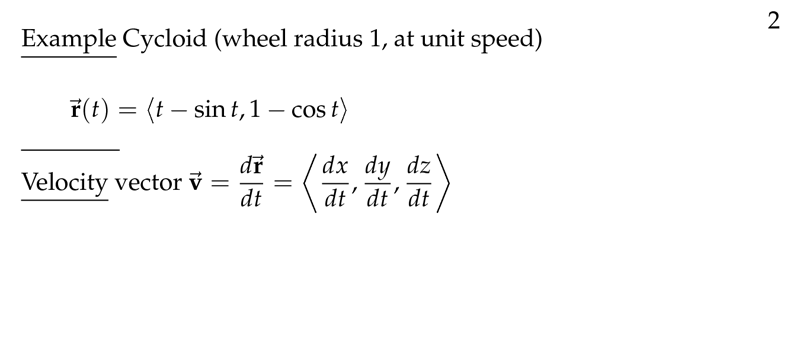
Figure 2: Velocity in a cycloid

Figure 3: Calculating module of speed
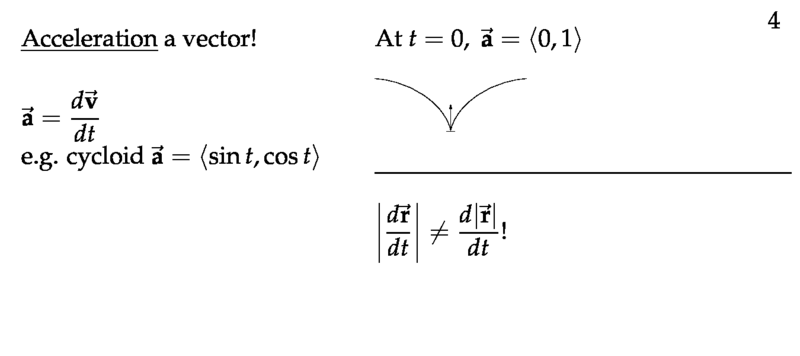
Figure 4: Acceleration a vector, and warning about derivative of a module
2 How can we get the velocity vector from a position vector?
2.1 Front
How can we get the velocity vector from a position vector?
Velocity definition and equation
2.2 Back
Velocity is the rate of change of the position respect to the time
\({\displaystyle \text{velocity} = \frac{d\vb{r}}{dt} = \frac{dx}{dt} \vb{i} + \frac{dy}{dt} \vb{j} = x’ \vb{i} + y’ \vb{j} = \ev{x’, y’}}\)
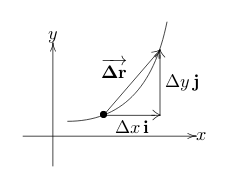
3 Why the velocity vector is the derivative of position vector?
3.1 Front
Why the velocity vector is the derivative of position vector?
3.2 Back
Velocity is the rate of change of the position respect to the time
\({\displaystyle \text{average velocity} = \frac{\Delta \vb{r}}{\Delta t} = \frac{\Delta x}{\Delta t} \vb{i} + \frac{\Delta y}{\Delta t} \vb{j}}\)
As \(\Delta t \to 0\), the average velocity becomes the instantaneous velocity, and the ratios becomes derivatives
\({\displaystyle \text{velocity} = \frac{d\vb{r}}{dt} = \frac{dx}{dt} \vb{i} + \frac{dy}{dt} \vb{j} = x’ \vb{i} + y’ \vb{j} = \ev{x’, y’}}\)
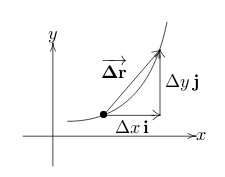
4 Which is the tangent vector of the position vector?
4.1 Front
Which is the tangent vector of the position vector?
- \(\vb{r(t)}\) is the position vector
4.2 Back
\({\displaystyle \text{tangent vector } = \frac{d \vb{r}}{dt}}\)
It’s the same as velocity, as \(\Delta t \to 0\), \(\frac{\Delta \vb{r}}{\Delta t}\) becomes tangent to the curve
Normally it’s called velocity, but geometrically it’s the tangent vector
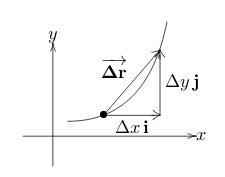
5 How can we get the acceleration of a position vector?
5.1 Front
How can we get the acceleration of a position vector?
\(\vb{r}(t)\)
5.2 Back
\({\displaystyle \text{acceleration} = \vb{a}(t) = \frac{d \vb{v}}{dt} = \frac{d^2 \vb{r}}{dt} = x’’(t) \vb{i} + y’’(t) \vb{j} = \ev{x’’, y’’}}\)
6 Is it the same meaning?
6.1 Front
Is it the same meaning?
\({\displaystyle \abs{\frac{d \vb{r}}{dt}} = \frac{d \abs{\vb{r}}}{dt}}\)
6.2 Back
Not, it is not the same. It \(\vb{r}\) is a vector position the first one it’s the module of the velocity vector (or tangent vector), the second one doesn’t mean anything
7 Get the angle in terms of time
7.1 Front
Get the angle in terms of time
Suppose that the wheel rolls at n revolution per seconds
7.2 Back
\(\theta(t) = t \cdot n \cdot 2 \pi\)
8 Which is the product rule for the derivative of a dot product?
8.1 Front
Which is the product rule for the derivative of a dot product?
2 parametric curves \(\vb{r_1}(t)\) and \(\vb{r_2}(t)\)
8.2 Back
Supposed in the same plane, but the proof is valid for curves in space
\({\displaystyle \frac{d (\vb{r_1} \cdot \vb{r_2})}{dt} = \vb{r_1}' \cdot \vb{r_2} + \vb{r_1} \cdot \vb{r_2}’}\)
You can proof with \(\vb{r_1} \cdot \vb{r_2} = x_1x_2 + y_1y_2\)
\({\displaystyle \frac{d (\vb{r_1} \cdot \vb{r_2})}{dt} = \frac{d(x_1x_2 + y_1y_2)}{dt}}\)
9 Which is the product rule for the derivative of a cross product?
9.1 Front
Which is the product rule for the derivative of a cross product?
2 parametric curves \(\vb{r_1}(t)\) and \(\vb{r_2}(t)\)
9.2 Back
\({\displaystyle \frac{d (\vb{r_1} \cross \vb{r_2})}{dt} = \vb{r_1}' \cross \vb{r_2} + \vb{r_1} \cross \vb{r_2}’}\)
Proof computing cross product, getting derivative of components, and aggregating by vectors
10 What does mean that the position vector has a constant length?
10.1 Front
What does mean that the position vector has a constant length?
\(\vb{r}(t)\) is the parametric curve
10.2 Back
It means that this point is moving in circles because of always stay at the same distance.
\(\vb{r} \cdot \vb{r} = c_1\), where \(c_1\) is constant
If we apply the derivative to this dot product, we can proof that the velocity vector is orthogonal to vector position, \(\vb{r} \cdot \vb{v} = 0\)
11 How can we show that a cross product is constant?
11.1 Front
How can we show that a cross product is constant?
Show that \(\vb{r} \cross \vb{v}\) is constant
11.2 Back
We can proof that through \({\displaystyle \frac{d}{dt} (\vb{r} \cross \vb{v}) = 0}\)
12 Can we say that it’s the same?
12.1 Front
Can we say that it’s the same?
\(\vb{r} \cross (c \vb{v}) = c (\vb{r} \cross \vb{v})\)
\(c\) is a scalar constant
12.2 Back
Yes, you can say that