1 Chalkboard
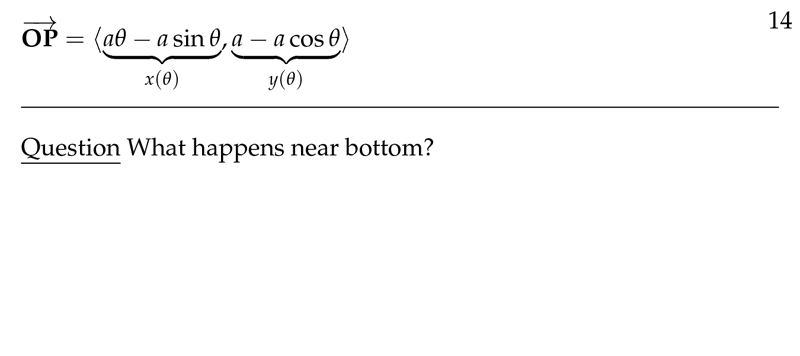
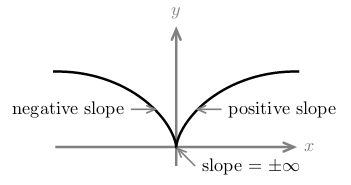
Figure 1: What happens near bottom?

Figure 2: Get an approximation for \(\theta\) small
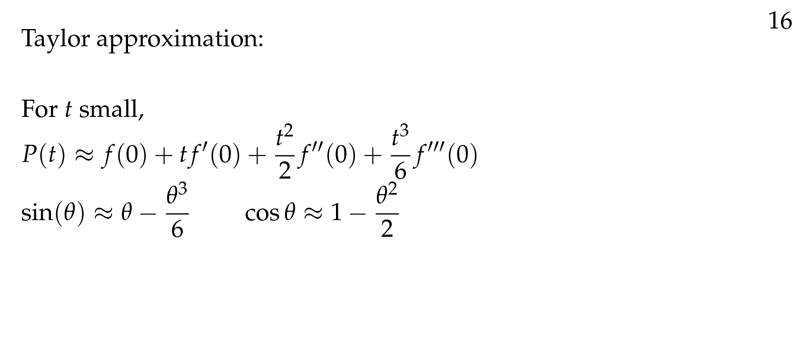
Figure 3: Taylor approximations for \(\sin\) and \(\cos\) when \(\theta\) is small
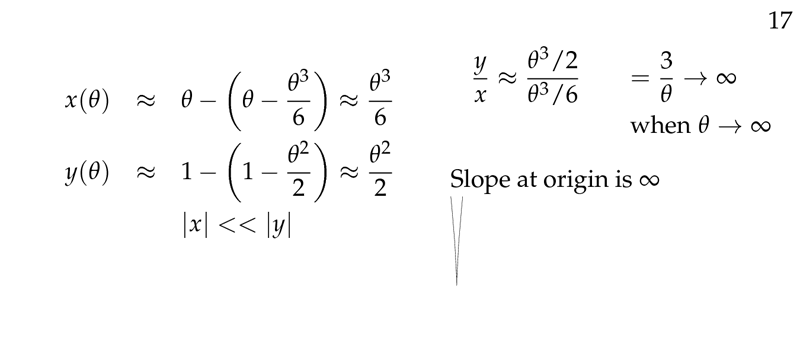
Figure 4: Slope when \(\theta\) is small
2 How can we analyze what happens at cusps on a cycloid graph?
2.1 Front
How can we analyze what happens at cusps on a cycloid graph?
The point where the graph of a cycloid touches the \(x\text{-axis}\) it’s called cusps
- Take radius \(1\), so the parametric equation
- \(x(\theta) = \theta - \sin \theta\)
- \(y(\theta) = 1 - \cos \theta\)
2.2 Back
Getting Taylor approximations near \(\theta = 0\) of \(\sin\) and \(\cos\)
You can also takes the derivatives
The slope of the curve is
\({\displaystyle \frac{dy}{dx} = \frac{dy/d\theta}{dx/d\theta} = \frac{\sin \theta}{1 - \cos \theta}}\)
As \(\theta \to 0\), \({\displaystyle \lim_{\theta \to 0} \frac{\sin \theta}{1 - \cos \theta}}\), that DNE (applying L’Hospital’s rule)