1 Chalkboard

Figure 1: Parametric equations for arbitrary motion (plane/space)
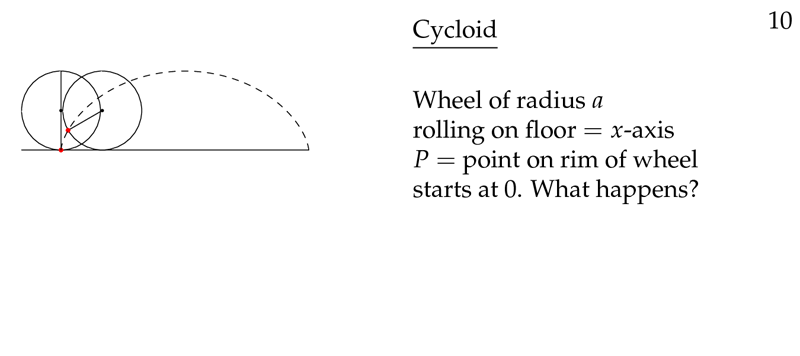
Figure 2: Cycloid path movement

Figure 3: Which is the position \((x(\theta), y (\theta))\)
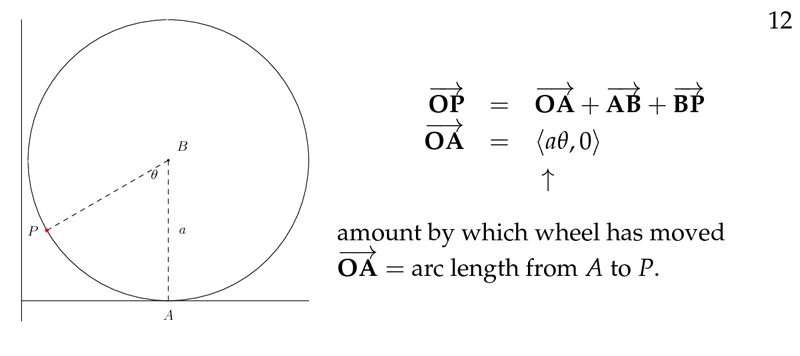
Figure 4: Vector position \(\vec{OP}\)
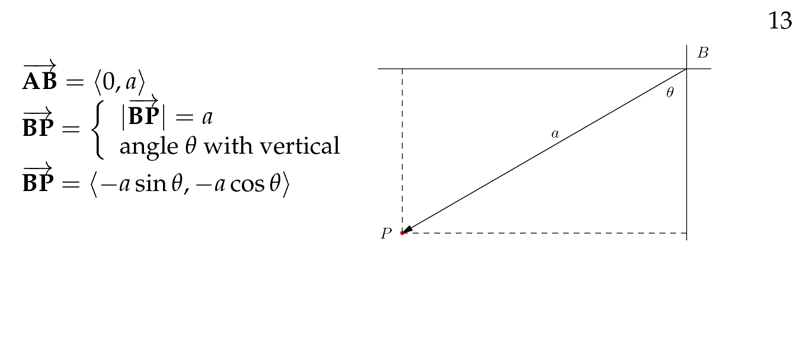
Figure 5: Getting vectors
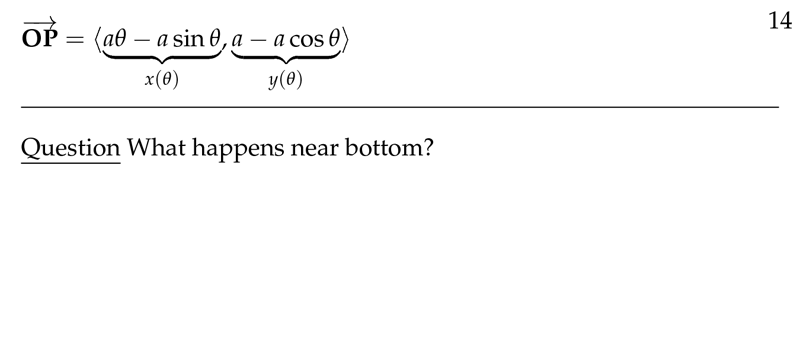
Figure 6: Vector position \(\vec{OP}\)
2 What is a cycloid?
2.1 Front
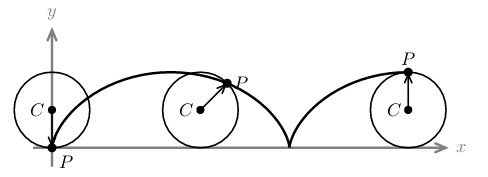
What is a cycloid?
2.2 Back
Is the trajectory of a point on a circle that is rolling without slipping along the \(x\text{-axis}\)
3 How can we get the vector position of a cycloid?
3.1 Front
How can we get the vector position of a cycloid?
3.2 Back
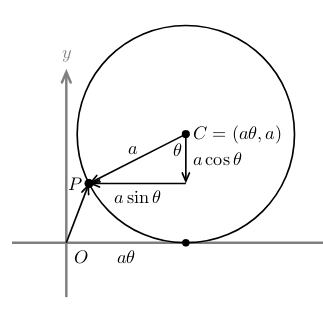
- \(\theta\) is the angle the wheel has turned
- \(\vec{OP}\) in terms of \(\theta\), not \(t\)
- \(\vec{OP} = \vec{OC} + \vec{CP}\)
After turning \(\theta\) radians, the wheel has rolled a distance \(a\theta\), so the center of the wheel is at \((a\theta, a)\), \(\vec{OC} = \ev{a \theta, a}\)
And position respect the center of the wheel, \(\vec{CP} = \ev{-a \sin \theta, -a \cos \theta}\)
So, \(\vec{OP} = \ev{a\theta - a \sin \theta, a - a \cos \theta} \Leftrightarrow x(\theta) = a\theta - a \sin \theta, y(\theta) = a - a \cos \theta\)
4 Which is the vector position of a helix?
4.1 Front
Which is the vector position of a helix?

4.2 Back
\(\vb{r}(t) = \cos t \hat{i} + \sin t \hat{j} + at \hat{k}\)