1 Chalkboard
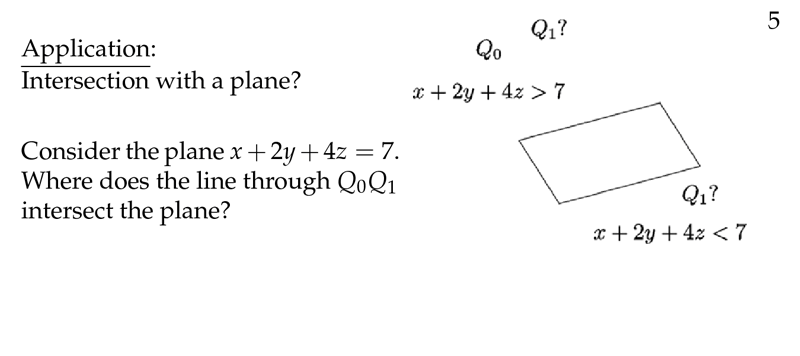
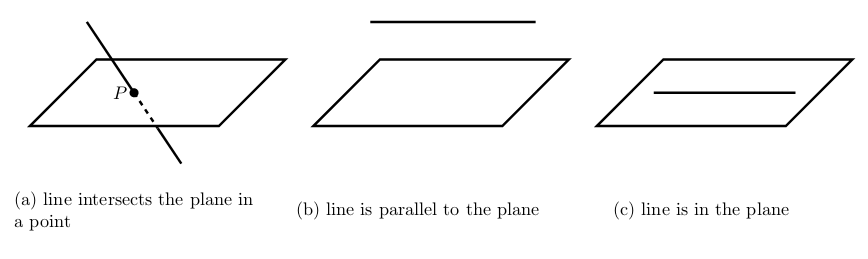
Figure 1: Application: Intersection with a plane
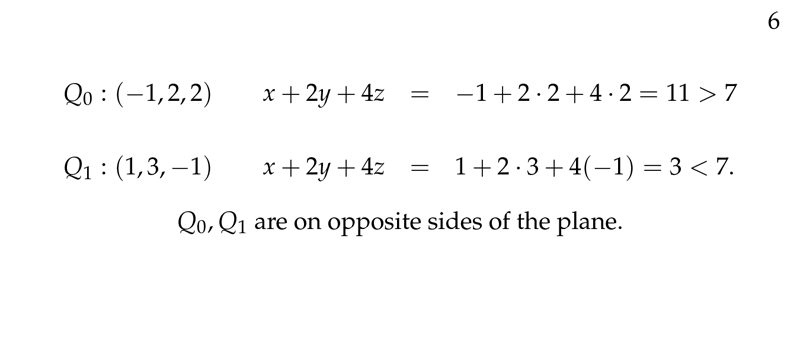
Figure 2: Where are the points respect to the plane?
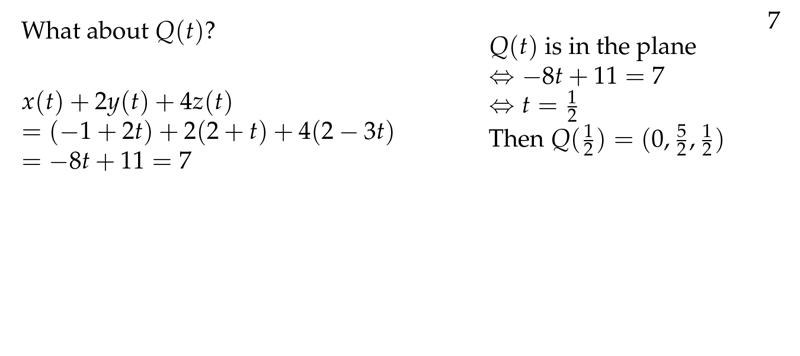
Figure 3: When will be an intersection to the plane?
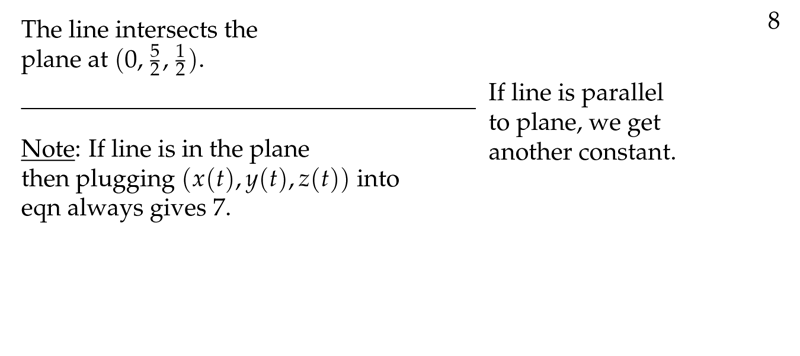
Figure 4: What does happen when the line is parallel to the plane or in the plane
2 How can we solve the intersection between a plane and a line?
2.1 Front
How can we solve the intersection between a plane and a line?
- Equation of a plane \(\mathcal{P}\)
- Parametric equation of a line
2.2 Back
We substitute the formulas for \(x\), \(y\) and \(z\) into the equation for \(\mathcal{P}\) and solve for \(t\). Depends on the values of \(t\) you get these kinds of solutions
- Get some specific \(t\)
- You get any constant different to \(\mathcal{P}\)
- You get a constant equals to \(\mathcal{P}\)
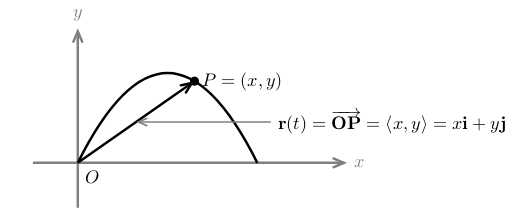
3 What is a position vector?
3.1 Front
What is a position vector?
Definition
3.2 Back
It’s a vector from the origin to the moving point. Used on parametric curves and describe where is the moving point respect to the origin. As the point moves so does the position vector
\(r(t) = x(t) \hat{i} + y(t) \hat{j} + z(t) \hat{k} = \ev{x(t), y(t), z(t)}\)
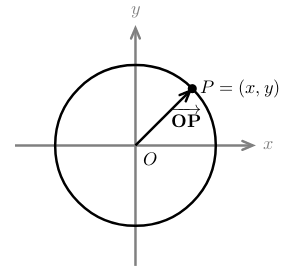
4 Which is the parametric curve of a circle from the origin?
4.1 Front
Which is the parametric curve of a circle from the origin?
4.2 Back
- \(x(t) = a \cos t\)
- \(y(t) = a \sin t\)
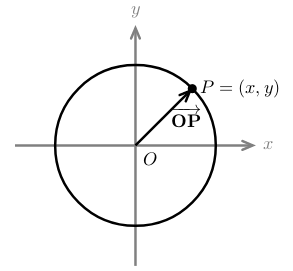
5 Which is the symmetric form of the equation of a circle from the origin?
5.1 Front
Which is the symmetric form of the equation of a circle from the origin?
5.2 Back
- \(x^2 + y^2 = a^2 \cos^2(t) + a^2 \sin^2(t) = a^2\)
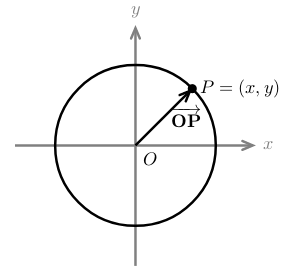
6 What is the vector position of the equation of a circle from the origin?
6.1 Front
What is the vector position of the equation of a circle from the origin?
6.2 Back
- \(\vec{OP} = \ev{a \cos t, a \sin t}\)
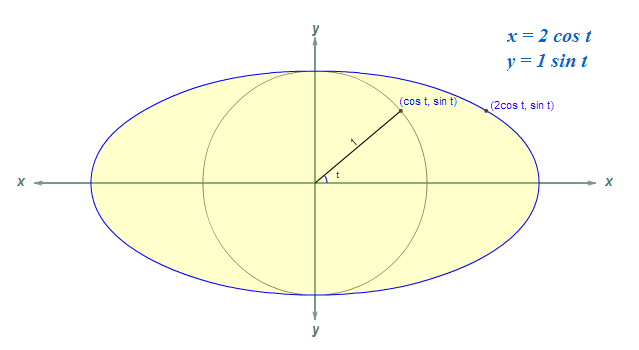
7 Which is the parametric curve of a ellipse at any point?
7.1 Front
Which is the parametric curve of a ellipse at any point?
- The center is shifted to \((h, k)\)
- \(a\) radius along \(x\text{-axis}\)
- \(b\) radius along \(y\text{-axis}\)
7.2 Back
- \(x(t) = h + a \cos t\)
- \(y(t) = k + b \sin t\)
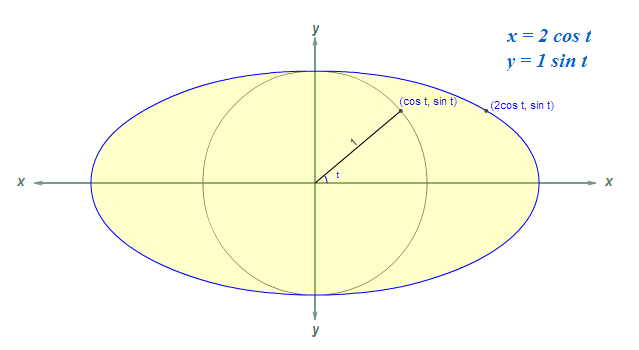
8 Which is the ellipse at any point?
8.1 Front
Which is the symmetric form of the equation of a ellipse at any point?
- The center is shifted to \((h, k)\)
- \(a\) radius along \(x\text{-axis}\)
- \(b\) radius along \(y\text{-axis}\)
8.2 Back
\({\displaystyle \frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} = 1}\)
9 Which is the vector position for line?
9.1 Front
Which is the vector position for line?
- Line through \((x_0, y_0)\)
- Parallel to vector \(\ev{b_1, b_2}\)
9.2 Back
\(\vb{r}(t) = \ev{x_0 + t b_1, y_0 + tb_2} = \ev{x_0, y _0} + t \ev{b_1, b_2}\)