1 Chalkboard
Figure 1: Equations of lines
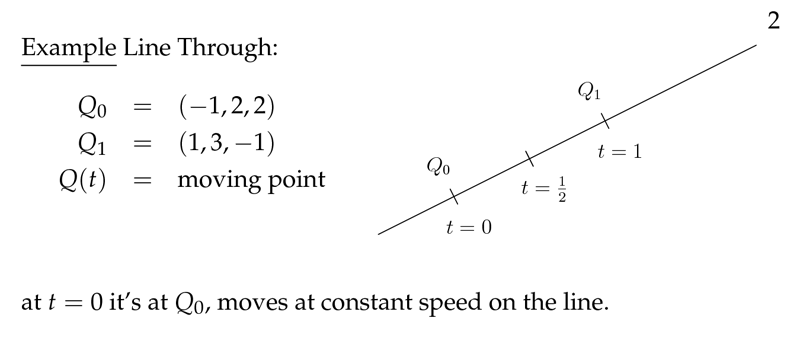
Figure 2: Example of line through 2 points
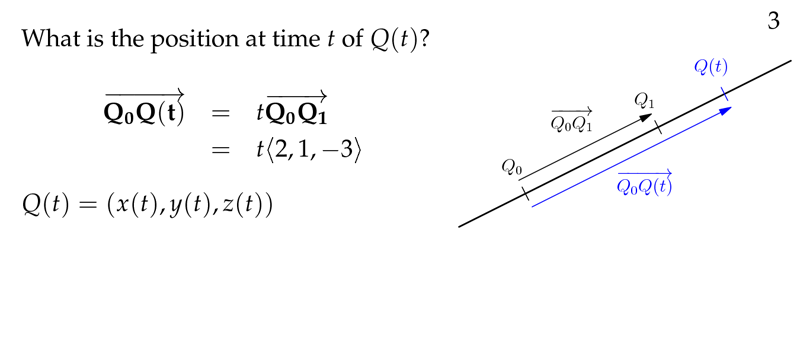
Figure 3: Position at time \(t\)
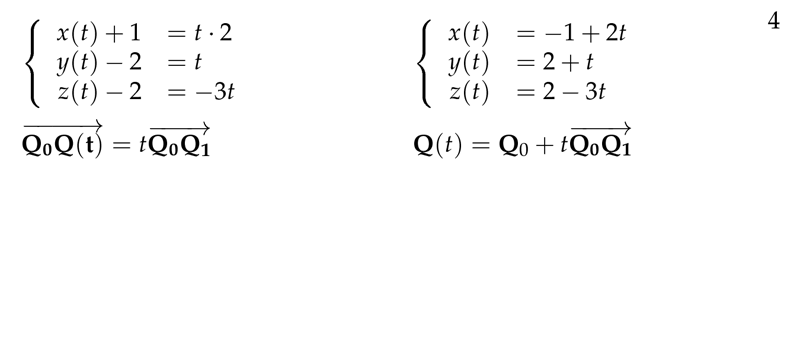
Figure 4: Get the parametric lines through 2 points
2 How does work a parametric curve?
2.1 Front
How does work a parametric curve?
Describe how traces a curve
2.2 Back
It’s a point moving in space traces out a path over time (an external variable). There are 3 position variables \((x,y,z)\) and independent variable \(t\), which we can think of as time
- \(x = x(t)\)
- \(y = y(t)\)
- \(z = z(t)\)
3 What does we need to creating a parametric equation of line?
3.1 Front
What does we need to creating a parametric equation of line?
3.2 Back
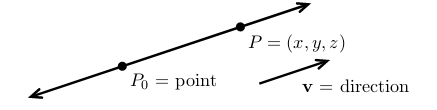
- Point \(P_0\) and an vector \(\vb{v}\)
- Independent variable \(t\)
- Any vector through this line to any point from \(P_0\) it’s proportional to \(t \cdot \vb{v}\)
- \(\vec{P_0P} = t \vb{v}\)
- \(\ev{x, y, z} = \ev{x_0 + t v_1, y_0 + t v_2, z_0 + t v_3}\)
4 How can we get the intersection line of 2 planes?
4.1 Front
How can we get the intersection line of 2 planes?
Result in parametric equation of line
4.2 Back
- Check that normal vectors are not parallel
- Get a point in this intersection. You can set an \(z\) axis to 0 an resolve the for \(x\) and \(y\)
- Line intersection is perpendicular to two normal vectors, so you get it through cross product
- Get the parametric lines with the point and direction vector of this line
5 How can we know that two points are in the plane or in different spaces?
5.1 Front
How can we know that two points are in the plane or in different spaces?
Point \(Q_0, Q_1\) are in the plane, two point in at one side of the plane or on opposite side of the plane
5.2 Back
- Check the point in the plane substituting \((x,y,z)\) with the point with the value of the plane
- Imagine as parallel planes, or 2 different spaces \(x + 2y + z < n\), or \(x + 2y +z > n\)