1 Chalkboard
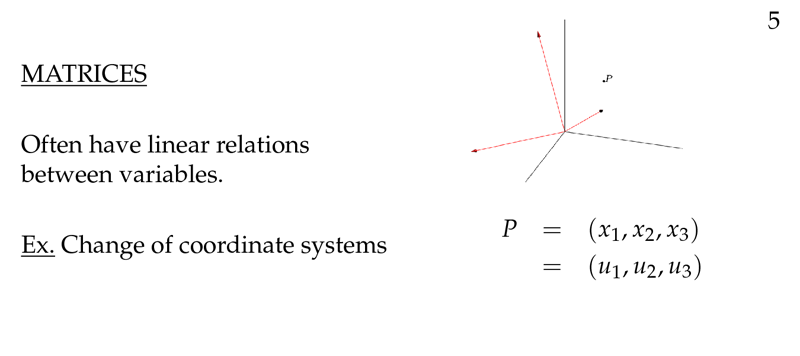
Figure 1: What is a matrix?
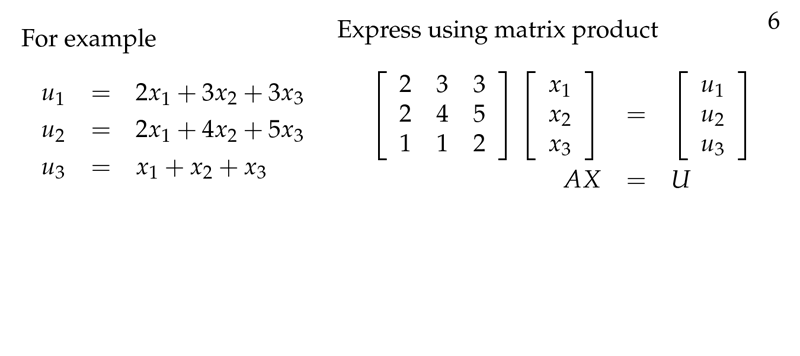
Figure 2: Change coordinate systems
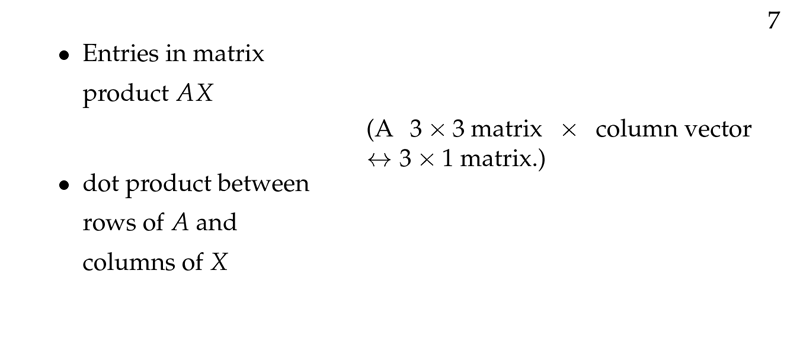
Figure 3: Entries in matrix multiplication
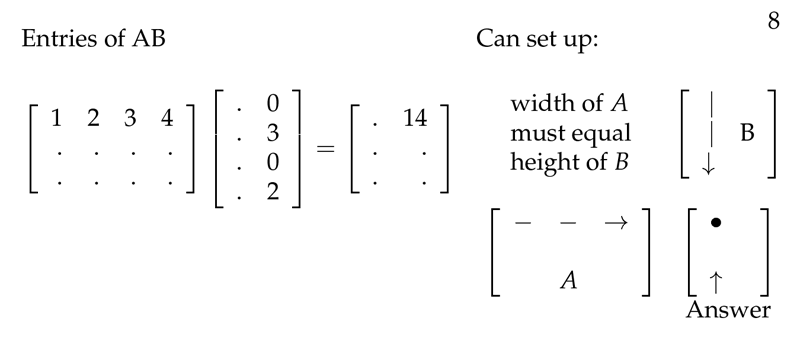
Figure 4: Nmemotecnic rule for matrix multiplication
2 How we can set up 2 matrix for its multiplication?
2.1 Front
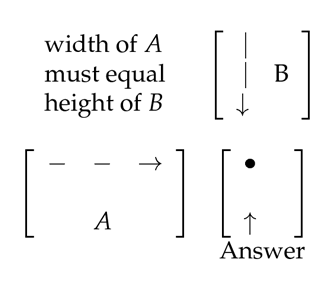
How we can set up 2 matrix for its multiplication?
I asking for the mnemonic rule of AB multiplication
2.2 Back
3 What kind of vector we form as a matrix?
3.1 Front
What kind of vector we form as a matrix?
3.2 Back
- row-vector as \(1 \times n\) matrix
- column-vector as \(m \times 1\) matrix
4 Matrix operations - Scalar multiplication
4.1 Front
Matrix operations - Scalar multiplication
\(cA\)
4.2 Back
\(cA = (ca_{ij})\)
- Multiply each entry
5 Matrix addition
5.1 Front
Matrix addition
A + B
5.2 Back
- The two matrix must have the same number of rows and the same number of columns
- Sum each entry of first matrix with the same entry of the other matrix
6 Matrix operation - Transposition
6.1 Front
Matrix operation - Transposition
6.2 Back
- Notation: \(A^T\), \(A’\)
- Making the rows of \(A\) the columns of the new matrix
- \(n \times m\) matrix \(\to\) \(m \times n\) matrix
- \(A^T = (a_{ji})\)