1 Chalkboard

Figure 1: Trivial solution and inverse of a matrix
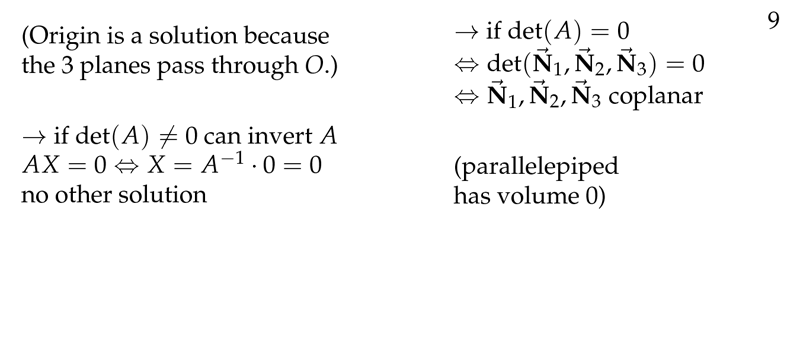
Figure 2: Solutions of homogeneous linear system

Figure 3: Coplanar normal vectors
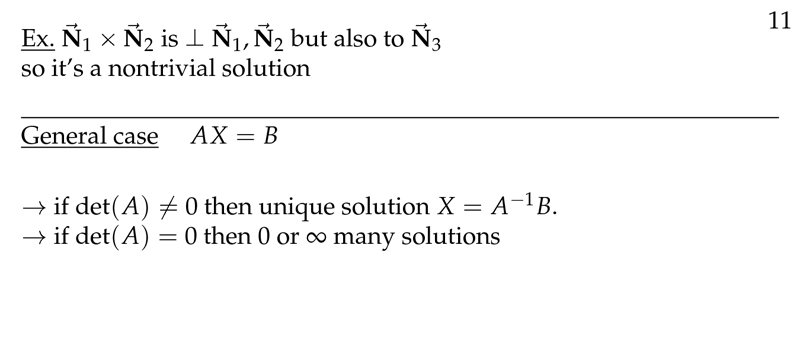
Figure 4: General case of solutions
2 When can we say that a linear system has an unique solution?
2.1 Front
When can we say that a linear system has an unique solution?
Let \(A\) be an \(n \times n\) matrix
2.2 Back
- \(\abs{A} \neq 0 \implies A\vb{x} = \vb{b}\) has the unique solution \(\vb{x} = A^{-1}\vb{b}\)
- \(\abs{A} \neq 0 \implies A\vb{x} = 0\) has only the trivial solution \(\vb{x} = 0\)
Also we can say
\(A \vb{x} = 0\) has a non-zero solution \(\implies \abs{A} = 0\)
3 What is a trivial solution in a linear system?
3.1 Front
What is a trivial solution in a linear system?
3.2 Back
\(\vb{x} = 0\)
4 What does happen when \(\abs{A}=0\) in a linear system \(A\vb{x}=0\)
4.1 Front
What does happen when $\abs{A}=0$ in a linear system $A\vb{x}=0$
Let \(A\) be represented by 3 row vectors, \(\vb{a}, \vb{b}, \vb{c}\), and let \(\vb{x} = \ev{x,y,z}\). Placing all of them at the origin.
Show up and compute a solution
4.2 Back
\(A \vb{x} = 0\), its equals to the system \(\vb{a} \cdot \vb{x} = 0\), \(\vb{b} \cdot \vb{x} = 0\), \(\vb{c} \cdot \vb{x} = 0\)
If \(\abs{A} = \vb{a} \cdot \vb{b} \cross \vb{c} = 0\), all row vectors are in the same plane, are coplanar. Any non-zero vector \(\vb{x}\) which is orthogonal to this plane will be orthogonal to \(\vb{a}, \vb{b}, \vb{c}\), and therefore will be a non-trivial solution to the system
If \(\vb{b} = 0\), has non-trivial solutions (non-zeros) solutions. \(\infty\) solutions
You can get the solution computing the cross product of 2 normal vectors of these planes, and getting any point of this line \((x,y,z) = \lambda (\vb{a} \cross \vb{b})\), where \(\lambda\) is any real number
5 When can we say that \(A\vb{x} = \vb{d} \neq 0\) has solutions if \(\abs{A}=0\)?
5.1 Front
When can we say that $A\vb{x} = \vb{d} \neq 0$ has solutions if $\abs{A}=0$?
5.2 Back
\(A\vb{x} = \vb{d} = \ev{d_1, d_2, d_3}\) can we write as \(\vb{a} \cdot \vb{x} = d_1\), \(\vb{b} \cdot \vb{x} = d_2\), \(\vb{c} \cdot \vb{x} = d_3\)
If \(\abs{A} = 0\), the normal vector of all planes are coplanar, so we can write one normal vector as a combination of the 2 others
\(\vb{c} = r \vb{a} + s\vb{b}\), where \(r, s\) are real numbers
\(\vb{c} \cdot \vb{x} = r(\vb{a} \cdot \vb{x}) + s(\vb{b} + \vb{x}) \implies d_3 = rd_1 sd_2\)
Unless the components of \(\vb{d}\) satisfy \(d_3 = r d_1 + s d_2\), there cannot be a solution; thus in general there are no solutions.
If \(\vb{d}\) satisfy \(d_3 = r d_1 + s d_2\), then the last equation on the linear system can be discarded. So, we need to check it the others 2 equations with 3 unknowns has non-zero solutions if they don’t represent two parallel planes.
6 What can we say about the solutions on inhomogeneous linear system?
6.1 Front
What can we say about the solutions on inhomogeneous linear system?
Let \(A\) be an \(n \times n\) matrix
6.2 Back
- Has the unique solution \(x = A^{-1}\vb{b}\) if \(\abs{A} \neq 0\)
- Usually has no solutions, but does have solutions for some \(\vb{b}\) if \(\abs{A} = 0\)
7 How can we write a line from a point and parallel to a vector?
7.1 Front
How can we write a line from a point and parallel to a vector?
Point: \(A\), and vector \(\vb{v}\)
7.2 Back
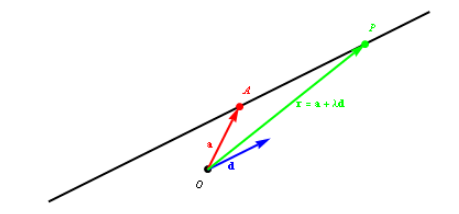
- Origin \(O\)
- Vector to point \(A\): \(\vb{a}\)
- Line: \(r = \vb{a} + \lambda \vb{v}\), where \(\lambda\) can we any real number
8 Which is the inverse of \((AB)^{-1}\)
8.1 Front
Which is the inverse of $(AB)^{-1}$
In terms of \(A^{-1}\) and \(B^{-1}\)
8.2 Back
\((AB)^{-1}= B^{-1} A^{-1}\)
Check by associative law and definition of the inverse
- \((B^{-1} A^{-1})(AB) = B^{-1}(A^{-1}A)B = B^{-1} I B = B^{-1}B = I\)
- \((AB)(B^{-1}A^{-1}) = A(B B^{-1})A^{-1} = A I A^{-1} = A A^{-1} = I\)
So, \(B^{-1}A^{-1}\) is the inverse to \(AB\)
9 What is the dihedral angle?
9.1 Front
What is the dihedral angle?
9.2 Back
This is the angle between 2 intersecting planes. You can calculate through the dot product of their normal vectors.