1 Chalkboard

Figure 1: 3x3 Linear System

Figure 2: Possible solutions to linear systems (2)
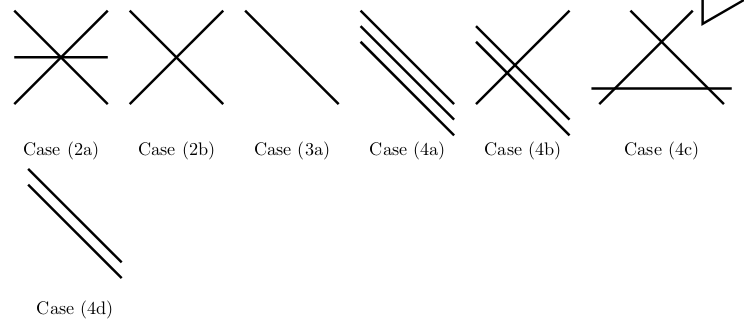
2 How many solutions we can get from a linear system?
2.1 Front
How many solutions we can get from a linear system?
And why
For lines and \(3 \times 3\) linear systems
2.2 Back
- Lines
- 2 lines intersect in a point (One solution)
- 2 lines are parallel (no solutions)
- 2 lines are the same (\(\infty\) solutions)
- 3x3 systems
- 3 planes intersect in a point (one solution)
- 3 planes intersect in a line (\(\infty\) solutions)
- 3 different planes, the 3rd plane contains the line of intersection
- 2 planes are the same, the 3rd plane intersect them in a line
- Intersect in a plane
- All three planes are the same
- The planes don’t all intersect at any point (no solutions)
- Different planes but parallel
- 2 parallel plane, the 3rd crosses them
- The planes are different and none are parallel, but the lines of intersection of each pair are parallel
- 2 planes are the same and 3rd is parallel
3 Write a linear system with no solution and where all planes are parallel
3.1 Front
Write a linear system with no solution and where all planes are parallel
3.2 Back
- Normal vectors are parallel
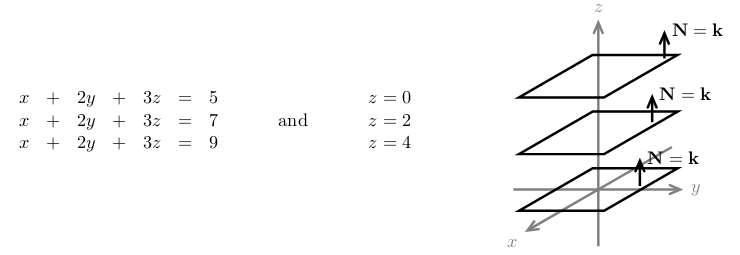
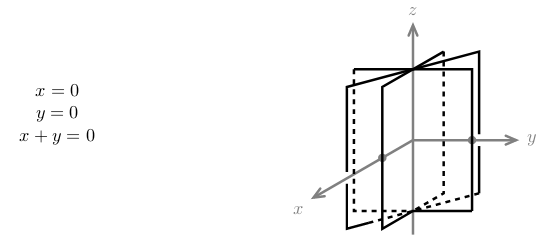
4 Write a linear system where the planes are all different and all intersect in a line
4.1 Front
Write a linear system where the planes are all different and all intersect in a line
4.2 Back
This is a little trickier. We’ll use a lot of zeros to help. The following system intersects in the \(z\text{-axis}\)
5 What is a homogeneous linear system?
5.1 Front
What is a homogeneous linear system?
Linear system: \(A\vb{x} = \vb{b}\)
5.2 Back
When \(\vb{b} = 0\), otherwise it’s called inhomogeneous