1 Chalkboard

Figure 1: Equations of Planes
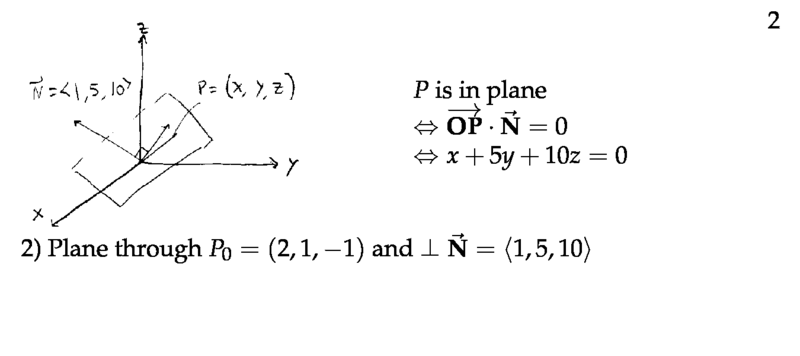
Figure 2: Point in the plane

Figure 3: Normal vector and vectors on the plane
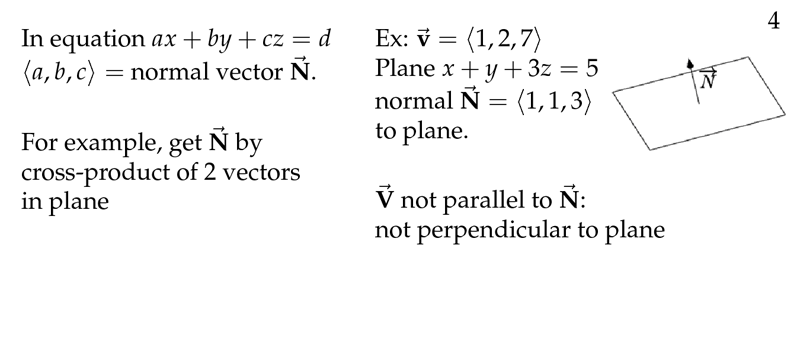
Figure 4: Extract normal vector from plane equation
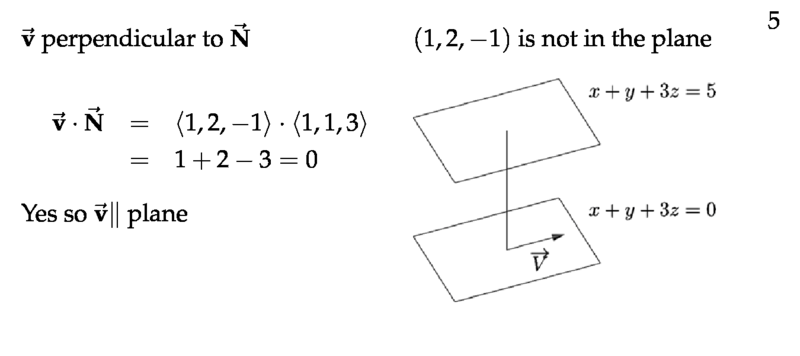
Figure 5: Check vector parallel or perpendicular to a plane
2 What do we need to determinate a plane?
2.1 Front
What do we need to determinate a plane?
2.2 Back
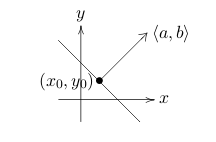
- Point \(P_0 = (x_0, y_0, z_0)\)
- Normal vector: \(\vb{N} = \ev{a,b,c}\)
- Orthogonal to the plane
- Let \(P = (x, y , z)\) arbitrary point in the plane
- \(\vec{P_0P}\) is orthogonal to \(\vb{N}\)
- \(\vb{N} \vec{P_0P} = 0\)
- \(\Leftrightarrow \ev{a,b,c} \cdot \ev{x - x_0, y - y_0, z-z_0} = 0\)
- \(\Leftrightarrow a(x - x_0) + b(y - y_0) + c(z - z_0)\)
- Quick version: \(ax + by + cz = ax_0 + by_0 cz_0\)
Also, you can determinate through 3 points in the plane, getting the normal through cross product between 2 vectors in the plane
With a point and 2 parallel vectors
3 How can we find an equation of a plane knowing all intercepts with the axis?
3.1 Front
How can we find an equation of a plane knowing all intercepts with the axis?
- Intercepts: \((a, 0 , 0)\), \((0, b, 0)\), \((0, 0, c)\)
3.2 Back
- Plane is \({\displaystyle \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1}\)
4 How can we find lines in the plane?
4.1 Front
How can we find lines in the plane?
- Describe 2 ways of write the equation of a line in the \(xy\text{-plane}\)
4.2 Back
- Slope-intercept form
- \(y = mx + b\)
- Point-normal form
- \(P_0 = (x_0, y_0)\)
- \(\vb{N} = \ev{a, b}\)
- \(a(x - x_0) + b(y - y_0) = 0\)
5 Can we extract the normal vector from the equation of a plane?
5.1 Front
Can we extract the normal vector from the equation of a plane?
\(x + 2y + 3z = -2\)
5.2 Back
\(\vb{N} = \ev{1, 2 ,3}\)
6 What is the equation of a plane from normal vector and 1 point?
6.1 Front
What is the equation of a plane from normal vector and 1 point?
- \(\vb{N} = \ev{a, b, c}\)
- \(P_0 = (x_0, y_0, z_0)\)
6.2 Back
\(ax + by + cz = ax_0 + by_0 + cz_0\)
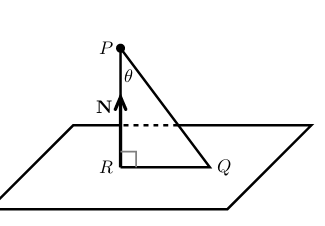
7 How can we calculate the distance to a plane from 1 point?
7.1 Front
How can we calculate the distance to a plane from 1 point?
- A point \(P\)
- Equation of a plane
7.2 Back
- A point \(P\)
- A plane with normal \(\vb{N}\) and containing a point \(Q\)
- Get any vector to the point \(P\) to point \(Q\) in the plane, doesn’t matter where this point is
- Get component of \(\vec{PQ}\) in direction of normal \(\vb{N}\) to the plane
- \({\displaystyle d = \abs{\vec{PQ}} \cos(\theta) = \abs{\vec{PQ} \cdot \frac{\vb{N}}{\abs{N}}}}\)
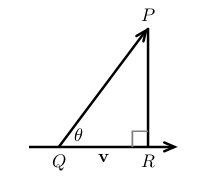
8 How can we calculate the distance: point to line?
8.1 Front
How can we calculate the distance: point to line?
- Point \(P\)
- Line with direction \(\vb{v}\)
8.2 Back
- Point \(P\)
- A line with direction \(\vb{v}\) and containing a point \(Q\)
- \({\displaystyle d = \abs{\vb{QP}} \sin \theta = \abs{\vb{QP}} \abs{\frac{\vb{v}}{\abs{v}}} \sin \theta = \abs{\vec{QP} \cross \frac{\vb{v}}{\abs{v}}}}\)
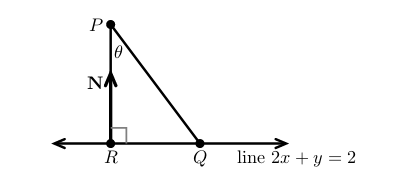
You can calculate the distance with the normal
- \({\displaystyle d = \abs{\vec{PQ} \cdot \frac{\vb{N}}{\abs{\vb{N}}}}}\)
9 How can we calculate the distance between 2 parallel planes?
9.1 Front
How can we calculate the distance between 2 parallel planes?
9.2 Back
- Reduce it to the distance from a point to a plane
- Get a normal vector to each plane, and check that they’re parallel each other
- Take any point from 1st plane
- Take any point the other plane
- \({\displaystyle d = \abs{\vec{QP} \cdot \frac{\vb{N}}{\abs{N}}}}\)