1 Chalkboard

Figure 1: What represent matrix multiplication
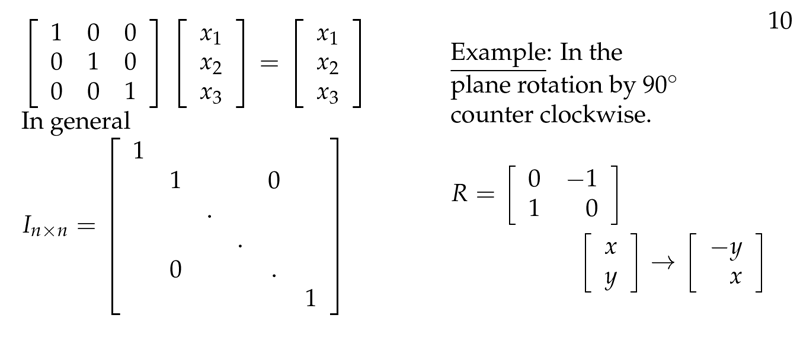
Figure 2: Matrix identity and plane rotation by matrix multiplication
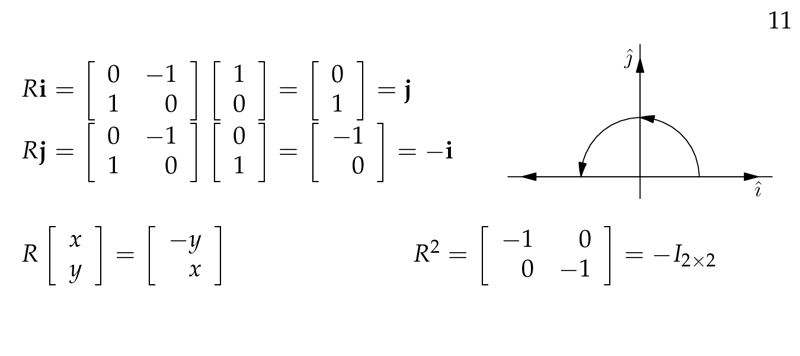
Figure 3: Continuous apply of rotation by matrix multiplication
2 Can we use the distributive law with matrix multiplication?
2.1 Front
Can we use the distributive law with matrix multiplication?
\(A(B + C) = AB + AC\)
2.2 Back
- Yes, it’s valid
3 Can we use the associative law with matrix multiplication?
3.1 Front
Can we use the associative law with matrix multiplication?
\((AB)C = A(BC)\)
3.2 Back
- Yes
4 Which is the identity matrix of order 3?
4.1 Front
Which is the identity matrix of order 3?
4.2 Back
- \(IA = AI = A\)
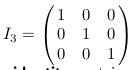
5 Can we use the commutative law with matrix multiplication?
5.1 Front
Can we use the commutative law with matrix multiplication?
\(AB = BA\)
5.2 Back
No, we can’t. The order it’s very important
- \(AB \neq BA\)
- Exception: when we are multiply be identity matrix
- \(AI = AI = A\)
6 Which is the determinant of the result of a matrix multiplication?
6.1 Front
Which is the determinant of the result of a matrix multiplication?
- \(|AB|\)
- \(\det(AB)\)
6.2 Back
- \(|AB| = |A||B|\)
- \(\det(AB) = \det(A) \det(B)\)
It’s difficult to proof with \(n \times n\) matrices
7 How we can get an specific row or column of a matrix?
7.1 Front
How we can get an specific row or column of a matrix?
Tip: Using matrix multiplication
7.2 Back
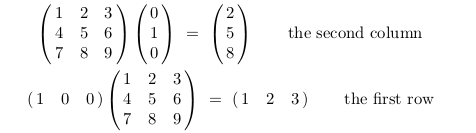
8 What are the laws and properties of matrix multiplication?
8.1 Front
What are the laws and properties of matrix multiplication?
Enumerate all laws and properties
8.2 Back
- Distributive law
- \(A(B + C) = AB + AC\)
- Associative law
- \((AB)C = A(BC)\)
- Identity matrix
- Diagonal of matrix is \(1\)
- No commutative law
- \(AB \neq BA\)
- Exception: \(IA = AI = A\)
- Determinant law
- \(|AB| = |A||B|\)
- \(\det(AB) = \det(A)\det(B)\)
- Extract one column or row
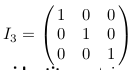
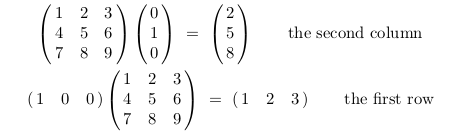
9 What are the matrix operations?
9.1 Front
What are the matrix operations?
Enumerate all matrix operations
9.2 Back
- Scalar multiplication
- Matrix addition
- Transposition
- Matrix multiplication
10 How can we show that one vector counterclockwise from another?
10.1 Front
How can we show that one vector counterclockwise from another?
It’s \(\vb{v_1}\) counterclockwise from \(\vb{v_2}\)
10.2 Back
- Using cross product
- \(\vb{v_2} \cross \vb{v_1}\)
- If it’s positive, \(\vb{v_2}\) counterclockwise from \(\vb{v_1}\)
- If it’s negative, \(\vb{v_2}\) clockwise from \(\vb{v_2}\)
11 What represent a matrix multiplication?
11.1 Front
What represent a matrix multiplication?
\(AB\)
11.2 Back
- Do transformation B, then transformation A
- Transformation is produced from right to left
- Similar to function composition