- Captured On
- Source
- Session 1: Vectors | Part A: Vectors, Determinants and Planes | 1. Vectors and Matrices | Multivariable Calculus | Mathematics | MIT OpenCourseWare
1 Chalkboard

Figure 1: Definition of vectors
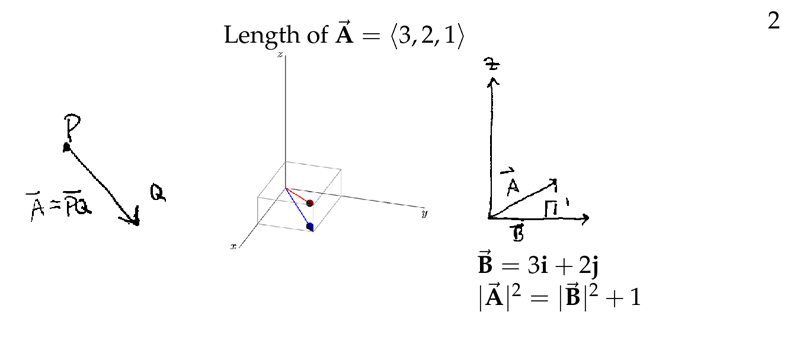
Figure 2: Length of a vector
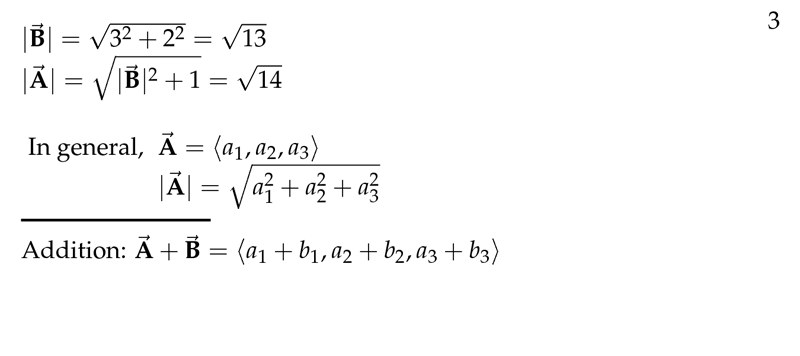
Figure 3: Modules and addition
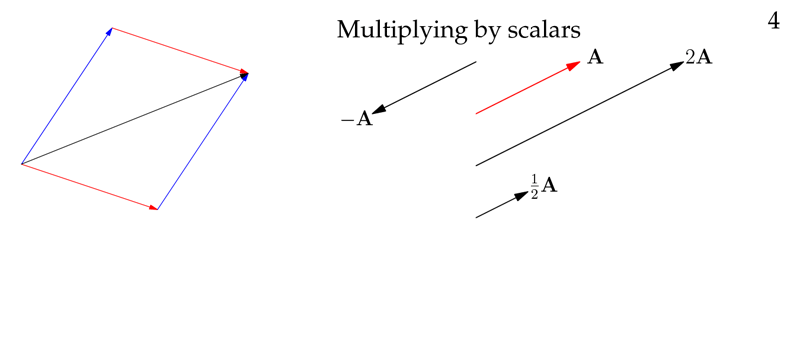
Figure 4: Multiplying by scalars
2 Which is the vector between 2 points?
2.1 Front
Which is the vector between 2 points?
For two points \(P\) and \(Q\)
2.2 Back
- \(\vb{PQ} = \vb{Q} - \vb{P}\)
- \(\vb{PQ}\) is the displacement from \(P\) to \(Q\)

3 Which is the notation for vectors and points?
3.1 Front
Which is the notation for vectors and points?
How we can write them?
3.2 Back
- Points: \((a_1, a_2)\)
- Vectors:
- \(<a_1, a_2> = a_1 \vb{i} + a_2 \vb{j}\)
- \({\displaystyle \vb{P} = \vb{OP}}\) is the vector from the origin to \(P\)
- A real number is a scalar
4 Which is the magnitude of a vector in 3D?
4.1 Front
Which is the magnitude of a vector in 3D?
\(\abs{\ev{a_1, a_2, a_3}}\)
4.2 Back

5 Which is a unit vector?
5.1 Front
Which is a unit vector?
5.2 Back
Is any vector with unit length \(\hat{u}\)
- \(\abs{\hat{u}} = 1\)
- Special vectors
- \(\hat{i} = \ev{1, 0, 0}\)
- \(\hat{j} = \ev{0, 1, 0}\)
- \(\hat{k} = \ev{0, 0, 1}\)
6 How can we get a vector of the median of the triangle?
6.1 Front
How can we get a vector of the median of the triangle?
Triangle: \(ABC\), from vertex: \(A\)
6.2 Back
\({\displaystyle \vb{AM} = \frac{1}{2} (\vec{B} + \vec{C}) - \vb{A}}\)
7 How we can find the unit vector from any vector?
7.1 Front
How we can find the unit vector from any vector?
7.2 Back
\({\displaystyle \hat{u} = \frac{\vb{u}}{|\vb{u}|}}\)